Researchers Demonstrate Quantum Entanglement Can Slash a 20-Million-Year Learning Task Down to Minutes
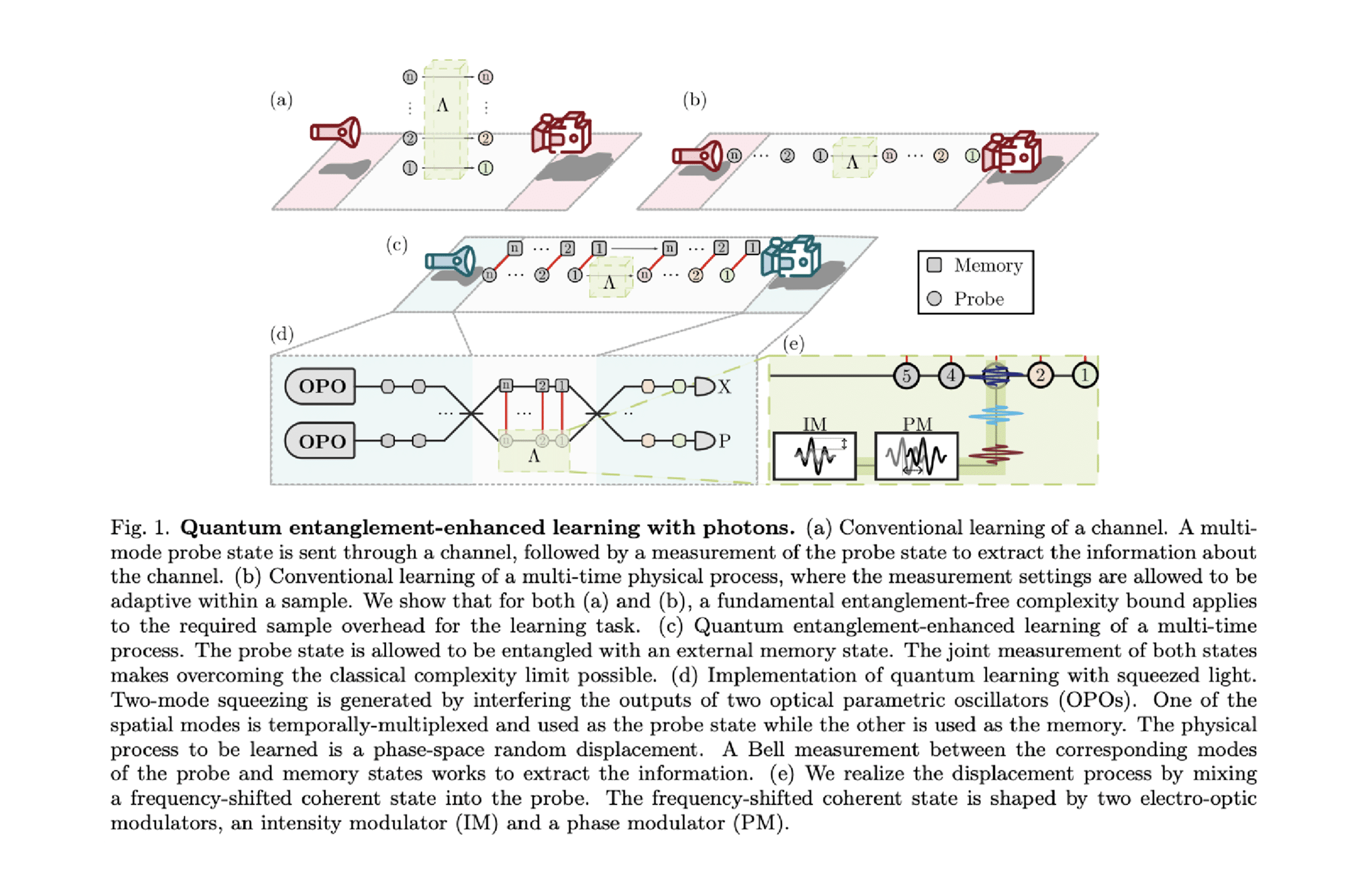
Table of Contents
25 Sep 2025 – A team led by the Technical University of Denmark (DTU) has published a milestone paper, “Quantum learning advantage on a scalable photonic platform,” in Science (Sept 25, 2025). Preprint arXiv:2502.07770. The work is the first proven quantum learning advantage using a photonic system, showing that an optical quantum setup can learn the behavior of a complex system exponentially faster than any classical method.
In their experiment, an information-gathering task that would take a classical approach on the order of 20 million years was completed in about 15 minutes using entangled light. This dramatic 11.8-orders-of-magnitude speedup in learning time highlights the power of quantum entanglement for practical data-driven tasks and marks an important step forward for quantum technologies in sensing and machine learning.
Quantum Advantage and Learning: A New Frontier
Quantum advantage refers to a quantum system outperforming the best possible classical computers on a well-defined task. Until recently, demonstrations of quantum advantage were limited to specialized computational problems. For example, in 2019 Google’s 53-qubit Sycamore processor performed a random circuit sampling calculation in 200 seconds that was estimated to take a classical supercomputer 10,000 years. In 2020, a photonic experiment in China (USTC) used boson sampling with 76 photons to perform a complex sampling task, claiming a quantum speedup factor of about 1014 over classical algorithms. These feats were groundbreaking, but they involved contrived math problems (random circuit sampling, boson sampling) with little direct application.
Quantum learning advantage is a newer concept, focusing on learning or inference tasks – for instance, learning the properties or “fingerprint” of a physical system from experimental data. Theoretical work has suggested that quantum techniques can learn from exponentially fewer experiments in certain scenarios.
The new Science paper by the DTU-led team brings quantum learning advantage into the realm of photonics. Unlike superconducting qubit processors that require extreme cryogenic cooling and complex control, photonic systems use particles of light and can operate at room temperature with standard optical components. This experiment is the first to leverage entangled light in a scalable optical setup to beat classical learning by an enormous margin. It shows that quantum advantage isn’t limited to big quantum computers – it can be realized with a “straightforward optical setup” in a lab, heralding a new avenue for practical quantum-enhanced learning protocols.
The Challenge: Learning a Complex Noise “Fingerprint”
At the heart of the study is a common problem in science and engineering: characterizing a complex system by measurement. For example, imagine trying to learn the noise characteristics of a new device or the random drift in a sensor. Classically, one must take many repeated measurements and analyze the outcomes to infer the underlying noise distribution – essentially mapping out a “noise fingerprint” of the system. As systems grow in complexity (more degrees of freedom, more parameters to learn), the number of experiments required can grow exponentially with the system size. This quickly becomes impractical or impossible – akin to trying to map every grain of sand on a growing beach, as one analogy puts it.
In quantum mechanical systems, the task is even tougher: not only might there be exponentially many configurations to sample, but quantum noise (the inherent uncertainty in quantum measurements) adds extra fuzziness to each measurement.
The specific learning task tackled in the new paper was to determine the probability distribution of a random bosonic displacement process acting on multiple modes of light. In simpler terms, the team set up an optical channel that imparts a random noise shift (a displacement in phase space) to each of many light pulses passing through it. The goal is to learn the entire distribution of these random shifts for a high-dimensional (multi-mode) system – essentially learning a complex noise pattern affecting 100 different modes of light.
Classically, learning such a high-dimensional noise distribution with the desired accuracy would require an astronomical number of measurements. In fact, the researchers estimate a conventional scheme would need on the order of 1012 more samples than their quantum strategy. To put that in perspective: the classical approach might take millions of years of data-taking, whereas the quantum approach finished the job in minutes. The stage was set to see if quantum entanglement could cut through this daunting sample complexity barrier.
Entangled Light as the Solution
The Danish-led team’s solution exploits one of quantum physics’ most powerful resources: entanglement. Entanglement is the mysterious linkage between particles (or light beams) such that measuring one immediately gives information about the other, no matter how far apart they are.
In practice, creating entanglement between two light beams was achieved using a device called a squeezer, or optical parametric oscillator (OPO), which uses a nonlinear crystal in an optical cavity to generate pairs of photons with correlated quantum fluctuations. The result is an Einstein-Podolsky-Rosen (EPR) entangled state – a pair of light modes whose amplitudes and phases are strongly correlated (often referred to as continuous-variable entanglement). In this experiment, about 4.8 dB of two-mode squeezing was used, which corresponds to a moderately strong entanglement between the twin beams. Notably, this entanglement is “imperfect” (no quantum state is noise-free), yet it proved sufficient to yield a huge advantage.
The experimental procedure is conceptually elegant. The researchers prepared two entangled beams of light. One beam – call it the probe – was sent through the noisy system (the optical channel imparting a random displacement). The other beam – the reference – did not go through the system and retained its original quantum state. Because of entanglement, however, the reference is not just an independent beam – it is strongly correlated with the probe beam at the quantum level. After the probe beam experiences the random noise in the channel, it carries information about that noise, but normally one would have to measure the probe many times to build up a statistical picture of the noise distribution. Here is where entanglement changes the game: instead of measuring the probe alone, the team performed a joint measurement on both the probe and reference together.
This joint measurement is essentially the continuous-variable analog of a Bell measurement, which projects two entangled particles onto correlated outcomes. In practice, the experiment combined the two beams on beam splitters and measured specific combinations of their light quadratures (amplitude and phase variables). By comparing the entangled twin beams in one shot, the measurement could “cancel out” much of the irrelevant noise (the random measurement fuzz) and extract far more information per trial about the channel’s effect than measuring the probe alone. Intuitively, because the reference beam was entangled with the probe before the probe went through the noise, the reference provides a baseline to directly see how the probe was disturbed. The entanglement ensures that any random disturbance from the channel stands out as a measurable difference between the two beams. This method allowed the experimenters to gain exponentially more information about the noise distribution from each experimental trial, dramatically reducing the number of trials needed overall.
11.8 Orders of Magnitude Fewer Samples: Results and Significance
The outcome of the experiment was unequivocal. In the primary task—reconstructing the full probability distribution of a 100-mode random displacement process—the quantum scheme used approximately 1011.8 times fewer samples than any conventional method.
In concrete terms, what might have been a 20-million-year data collection ordeal for classical methods was finished in about 15 minutes. The team further solidified this claim by demonstrating a provable quantum advantage in a more rigorous hypothesis-testing task. Here, for a 120-mode process, the quantum approach was 109.2 times more efficient, a speedup that is mathematically guaranteed to be impossible for any classical strategy. This stunning gap highlights the fundamental power of entanglement for learning. It provides a clear “before-and-after” illustration of entanglement’s power: entangled light turned an otherwise unfeasible learning problem into one solvable in real time. As Prof. Ulrik Lund Andersen, the corresponding author, put it, “We learned the behavior of our system in 15 minutes, while a comparable classical approach would take around 20 million years”.
Crucially, this quantum advantage was achieved without extreme hardware requirements. The experiment ran in a basement lab using telecommunications-wavelength light and standard optical components (lasers, nonlinear crystals, beam splitters, photodetectors). It was also tolerant to losses (around 20%) and imperfections present in the optical setup, meaning it did not rely on a near-perfect, isolated quantum system.
This robustness is important – it shows that the huge performance gain comes from the measurement strategy (entangled probes + joint detection) rather than from using a physically flawless device. In other words, even with “ordinary losses” in the system, the entanglement-enabled protocol still beats any classical strategy. This addresses a frequent skepticism in quantum advantage claims, where often the experiments work only in idealized conditions. Here, the team demonstrated a verifiable advantage in spite of real-world noise and imperfections, underlining the result’s practicality.
Another point of significance is highlighted by co-author Jonas Schou Neergaard-Nielsen: this is a quantum mechanical system doing something no classical system ever will be able to do. The phrasing “no classical system will ever do” is a strong claim. It reflects that the task they solved is not just faster on quantum hardware – it is provably intractable on any classical device for large system sizes (because classical sample complexity scales exponentially with system dimension).
The experimenters essentially checked off all the boxes for a true quantum advantage demonstration: a well-defined task with known classical complexity, a quantum method that asymptotically outperforms, and an experimental realization of that method at a scale where the quantum wins outright. This firmly moves the discussion from “quantum advantage is coming” to “quantum advantage is here”, at least for this class of learning problems.
A Scalable and Practical Photonic Platform
A key aspect of this work is the scalability and practicality of the photonic platform they used. Photonics is considered a promising route for scaling up quantum technologies because photons can be generated, manipulated, and detected with low noise at room temperature, and can be multiplexed in time or frequency to handle many modes. The DTU experiment operates at standard telecom wavelengths (around 1550 nm), meaning the setup is compatible with existing fiber-optic infrastructure and components. The use of off-the-shelf optical parts (“well-known optical parts” as the authors say) implies that no exotic new hardware needed to be invented for this demonstration – the innovation was in how those parts were configured and used (i.e. the protocol design).
Scalability in this context comes from the fact that generating entangled light and distributing it across many modes can be done with known techniques. For instance, a single OPO device can produce entanglement across many pairs of modes (by squeezing multiple frequency comb lines or successive time pulses), and photonic circuits can in principle route and mix hundreds of modes. Indeed, the paper explicitly learned a 100-mode noise process – indicating the experiment already dealt with high-dimensional data. In conventional quantum computing, handling 100 modes or qubits with full quantum correlations would be very challenging; here it was achieved with a table-top optical setup. This suggests that adding more modes to tackle even larger problems is feasible by simply extending the photonic network or using multiple entangled sources. The fact that only 5 dB of squeezing (entanglement strength) was needed and that the system tolerated loss also bodes well for scaling: higher squeezing or better detectors could further improve performance, but are not strictly required to surpass classical methods by a huge margin.
The authors describe their setup as “scalable” in the title for good reason. Photonic entanglement can be distributed over long distances (for networking) or across many channels in parallel, which could enable quantum-enhanced sensing networks or large-scale quantum data analysis systems. Additionally, unlike massive supercomputers or dilution refrigerators for qubits, an optical system at telecom wavelength can be relatively compact and even integrated on photonic chips. All these factors make the approach attractive for real-world deployment. As Ulrik Lund Andersen noted, seeing a quantum advantage with a “straightforward optical setup” should encourage researchers to seek other applications where this approach of entangled probes could payoff, for example in precision sensing or in machine learning tasks involving big data.
Implications for Quantum Technology and Future Applications
Beyond its headline result, this research carries several encouraging implications:
- Quantum Metrology & Sensing: The experiment essentially performed a metrology task (estimating a noise distribution) with unprecedented efficiency. This hints that quantum sensors could be designed to detect tiny signals or changes with far fewer readings than classical sensors would need. For example, one could envision entangled light probes enhancing gravitational wave detectors, magnetic field sensors, or other instruments, allowing them to reach a given sensitivity faster or with fewer repetitions. The authors specifically mention that approaches like theirs could make quantum sensors operate with “unprecedented efficiency” in detecting minute effects.
- Machine Learning and System Identification: Many machine learning algorithms face the challenge of learning patterns from high-dimensional, noisy data. The demonstrated protocol can be seen as a quantum feature extractor that pulls out information more efficiently than classical sampling. In scenarios where data is expensive or slow to obtain (e.g. characterizing a complex new material or a quantum device’s error profile), entangled probe techniques could dramatically reduce the data requirements. While today’s result was in a controlled setting, it paves the way for applying quantum-enhanced learning to real-world systems – potentially speeding up tasks in anything from drug discovery to climate modeling that involve learning the behavior of complex, stochastic systems. These possibilities remain to be fleshed out, but the door is now open.
- Quantum Computing Architecture: This success of a continuous-variable photonic system highlights an alternative route to quantum information processing. Most public attention goes to discrete qubit platforms (superconducting, trapped-ion, etc.), but photonic continuous-variable systems can also deliver quantum advantages. They might do so in a more hardware-friendly way for certain tasks. The fact that today’s photonic experiment achieved a huge advantage with no error correction and with noise present is a proof-of-concept that some quantum computational benefits can be reaped prior to full-scale fault-tolerant quantum computers. It suggests a hybrid future where special-purpose quantum photonic devices tackle specific hard problems (like system learning, optimization, sampling) alongside general quantum computers.
- Near-Term Quantum Advantage: Perhaps most importantly, this work is a “proof point” that quantum advantage is not just a theoretical speculation but is achievable with current technology. The researchers translated a recent theoretical proposal (from their 2024 paper on entanglement-enhanced learning) into a working experiment within about a year. This rapid turnaround from theory to demonstration indicates that we may soon see more quantum advantage experiments targeting useful tasks. It encourages a mindset shift: instead of assuming we must wait for thousands of error-corrected qubits for any real quantum benefit, we can ask “What useful problem can I solve today with the quantum resources I can entangle or control?” The DTU-led team identified one such problem (learning a complex noise process) and solved it with current photonic tech. Others might find different high-value problems suitable for a similar treatment.
In summary, “Quantum learning advantage on a scalable photonic platform” is a landmark in showing how quantum entanglement can revolutionize the way we acquire information about the physical world. By reducing a multi-million-year learning problem to minutes, the experiment dramatically illustrates the gap between classical and quantum capabilities for specific tasks. Equally important, it does so on a practical, scalable platform – standard laser optics and detectors – making the achievement not just a theoretical curiosity but a prototype of quantum advantage that could be deployed in real-life settings.
Quantum Upside & Quantum Risk - Handled
My company - Applied Quantum - helps governments, enterprises, and investors prepare for both the upside and the risk of quantum technologies. We deliver concise board and investor briefings; demystify quantum computing, sensing, and communications; craft national and corporate strategies to capture advantage; and turn plans into delivery. We help you mitigate the cquantum risk by executing crypto‑inventory, crypto‑agility implementation, PQC migration, and broader defenses against the quantum threat. We run vendor due diligence, proof‑of‑value pilots, standards and policy alignment, workforce training, and procurement support, then oversee implementation across your organization. Contact me if you want help.