First Unconditional Quantum Information Supremacy: 12 Qubits vs 62 Classical Bits
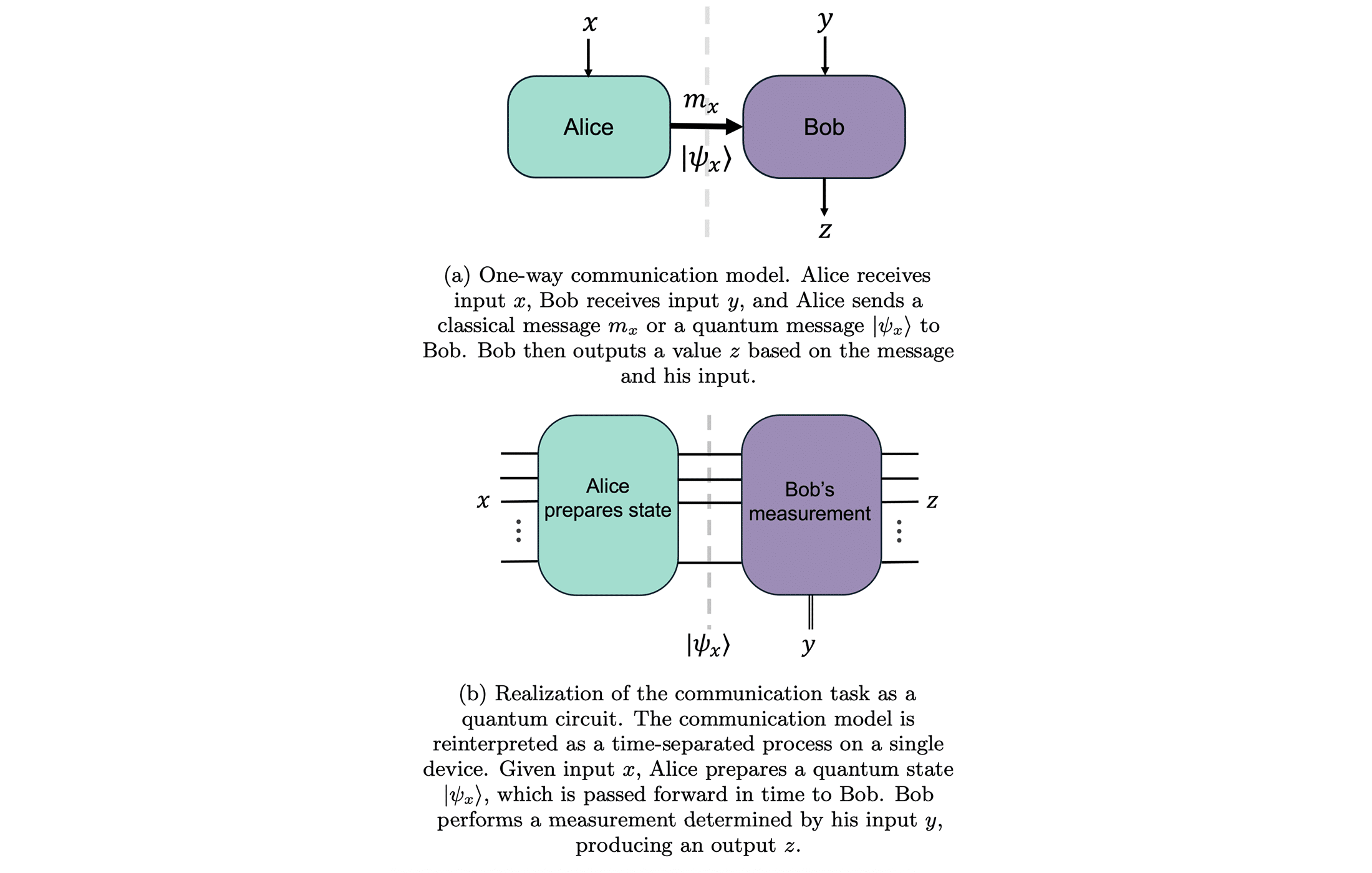
Table of Contents
Sep 2025 – A team of researchers from the University of Texas at Austin and Quantinuum has achieved a landmark result in quantum computing. Just published in Kretschmer et al., “Demonstrating an Unconditional Separation Between Quantum and Classical Information Resources,” arXiv preprint (Sep 2025). They demonstrated a computational task on a 12-qubit trapped-ion quantum system that no classical computer can emulate without using at least 62 bits of memory. This represents the first unconditional quantum advantage ever shown experimentally – a breakthrough the authors term “quantum information supremacy.” Unlike prior claims of quantum supremacy, which relied on conjectures about classical complexity, this result comes with a provable guarantee: no future clever algorithm or hardware improvement can close the quantum-classical gap for this task. In short, it’s permanent proof that current quantum hardware can access information-processing resources that classical systems fundamentally cannot.
From Quantum Supremacy to Quantum Information Supremacy
The notion of quantum supremacy (or quantum advantage) refers to a quantum computer demonstrably outperforming classical computers on some problem. Google’s Sycamore processor famously claimed this in 2019 by sampling random quantum circuits faster than a supercomputer could. Similarly, USTC in China reported quantum advantage in photon-based boson sampling and superconducting circuits. However, those pioneering experiments came with big caveats. They were essentially betting on certain problems being hard for classical computers – a bet based on complexity theory conjectures rather than proven facts.
Critics noted that improved classical algorithms or more efficient simulations might erode or even eliminate the advantage, and indeed subsequent optimizations did narrow some of those gaps. In other words, previous “quantum supremacy” demonstrations were conditional – their validity depended on assumptions that hadn’t been formally proven, leaving room for debate and doubt.
Quantum information supremacy, as defined by Kretschmer et al. (2025), is a new benchmark meant to address those shortcomings. In this experiment, the quantum advantage is backed by a mathematical proof rather than a complexity assumption. The researchers prove that any classical approach to the chosen task would require a certain minimum amount of memory (measured in bits) to achieve the same performance. If a classical algorithm doesn’t have those bits available, it simply cannot match the quantum device’s success – not because we think it’s hard, but because it’s impossible by fundamental bounds. This makes the quantum advantage unconditional and immune to future classical improvements. Unlike most quantum supremacy claims, in this case it is impossible to find a better classical algorithm.
A 12-Qubit Task That Classical Bits Can’t Match
The core achievement is succinct: a 12-qubit quantum system solved a task that any classical computer would need between 62 and 382 bits of memory to solve with comparable success. In the actual experiment, the team showed that even to approach the quantum device’s output quality, a classical simulation would require at least 78 bits of memory on average, and no less than 62 bits even under generous assumptions. To put it plainly, a dozen qubits outperformed what dozens (or even hundreds) of classical bits can do in the same scenario. This gap is small in absolute terms – modern computers have plenty of bits – but it’s hugely significant as a proof-of-principle. It validates that quantum states really do carry an exponentially richer information content: those 12 qubits reside in a Hilbert space of dimension $$2^12$$ (about 4096), and the experiment forced classical bits to play catch-up with that large state space.
Equally important is the metric used to compare quantum and classical performance. The team implemented a task where the goal is to produce outputs with a high linear cross-entropy benchmarking (XEB) fidelity – essentially a score indicating how closely the output distribution matches the true quantum-mechanical prediction. If a device outputs completely random results, the XEB fidelity is 0; a perfect quantum device would score near 1. Google’s 53-qubit supremacy experiment, for example, achieved a tiny XEB fidelity (~0.002) yet still claimed quantum advantage, because even that small signal was (at the time) out of reach for classical simulation.
In the new 12-qubit experiment, thanks to the device’s high precision, the average XEB fidelity was a much higher 0.427 (42.7%). This means the quantum outputs had a strong correlation with the ideal expected probabilities. Hitting this fidelity with 12 qubits triggers the theoretical bound that any classical protocol would need on the order of $$2^12$$ bits of memory – indeed they prove 62 bits minimum – to get an equivalent score. In practice, using about 330 classical bits of memory can reproduce the quantum’s 0.427 fidelity, and 382 bits could push slightly beyond it. But a classical algorithm with, say, only 50 bits of total state would fall far short. The numbers 12 vs 62 may not sound astronomical, but this gap is formally unbridgeable without those extra bits, firmly establishing the reality of the quantum advantage in this regime.
How Did They Do It? A One-Way Communication Task Reimagined
The experiment’s design is rooted in a concept from theoretical computer science called one-way communication complexity. In a standard setting, we imagine two parties: Alice receives some input data x, Bob gets some input y, and Alice is allowed to send a single message to Bob (one-way) to help him produce an answer z for a given task. The question is: how many bits must that message contain for them to succeed? Quantum theory adds a twist – what if Alice can send qubits (a quantum state) instead of classical bits? Years of research have shown that for certain tasks, a quantum message can be exponentially more efficient than a classical one. The team leveraged one of these tasks to demonstrate a separation in the lab.
They formulated a specific one-way communication problem that meets all the criteria for showcasing quantum advantage on real hardware. In their task, Alice’s goal is to send Bob a message that helps him output samples z that have a high probability under a certain distribution (essentially, Bob tries to guess outcomes that “look like” they came from measuring Alice’s state). Formally, it’s described as a distributed cross-entropy heavy output generation (DXHOG) problem. Here’s how it works in simple terms:
- Alice receives a description of an n-qubit quantum state |ψ⟩ (drawn from some distribution). Bob receives a description of a random quantum measurement (unitary U) he should perform.
- Alice sends a message to Bob based on her state. In the quantum protocol, that message is literally the quantum state |ψ⟩ itself, encoded into n qubits. In a classical protocol, Alice would have to send some number of classical bits describing what she knows.
- Bob then applies his measurement U to the state (if he received qubits) and records an outcome z. The aim is that z is more likely to be one of the “heavy” outputs – those with above-average probability for the distribution defined by |ψ⟩ and U. In practice, they score the success using the XEB fidelity of the output distribution.
By reinterpreting this as a single device experiment, the researchers didn’t actually have two separate parties sending physical messages. Instead, they treated the quantum processor at different times as “Alice” and “Bob.” First the device prepared Alice’s 12-qubit state |ψ⟩; then (after some delay and the setting of some classical controls) the device applied Bob’s measurement U and produced an outcome. This clever time-separation ensured that no outside classical computer was assisting during the quantum evolution – the quantum device essentially had to “carry” the necessary information in its qubits from the state-preparation stage to the measurement stage, rather than a classical memory carrying it.
Crucially, the chosen task has a known theoretical lower bound: any classical one-way protocol that achieves a non-negligible XEB fidelity ε on this problem must send on the order of $$2^n$$ bits (in general). For the parameters they used (n = 12 qubits and achieved ε ≈ 0.427), the proven bound works out to dozens of bits, as noted earlier. This is why a 12-qubit quantum message can succeed where a 12-bit classical message fails – in fact, even a 60-bit message isn’t enough in principle. The experiment thus becomes a direct test of this theoretical gap.
They ran 10,000 independent trials of this Alice/Bob protocol on the quantum machine, each time with fresh random inputs (random quantum state, random measurement choice). Importantly, true randomness was used: a hardware random number generator provided the random bits to ensure there was no subtle pattern that a classical simulator could exploit. Across all those trials, the quantum device achieved an average XEB fidelity of 0.427(13) – a clear signal well above zero, indicating the device was indeed doing something highly structured that random guessing could not replicate. According to their theorem, plugging n=12 and ε=0.427 implies any classical strategy with fewer than 78 bits of communication (memory) on average would fail to reach that fidelity. Even accounting for statistical uncertainty (to 5 standard errors), one would still require at least 62 bits in a classical protocol, which was the headline claim.
Why This Result Is Especially Credible
Several aspects of the experiment make it an unusually convincing quantum advantage demonstration, addressing concerns raised about earlier claims:
- Provable Classical Limit: The separation is backed by a theorem, not just a conjecture. The authors proved that any classical algorithm achieving the same performance needs a large memory (62+ bits). This means the quantum advantage doesn’t rest on unproven assumptions about computational complexity – it’s on firm theoretical ground. No matter how clever classical programmers get, they cannot circumvent this bound without violating known results.
- True Random Inputs: Every trial used fresh unpredictability. The random states |ψ⟩ and measurements U were drawn from genuine hardware random numbers, because the classical lower bound only holds for uniformly random inputs. Using a pseudo-random generator could, in principle, have allowed a classical adversary to exploit hidden structure. By using a high-quality quantum random number source, the experiment closed that loophole and strictly matched the theoretical conditions.
- Noise Tolerance and Modeling: The task and protocol were designed to be robust against the device’s noise. The researchers performed extensive noise modeling and chose an approach (like using Clifford measurements and a variational state prep) that the hardware could execute with high fidelity. The achieved fidelity (≈0.43) was well above the noise floor, and they verified that this fidelity correlates well with the theoretical XEB metric as expected. In fact, they showed that even if the quantum device were somewhat noisy, as long as it produces a nonzero XEB score, the classical memory bound still holds proportionally. This means the advantage is noise-tolerant – it doesn’t require a perfect quantum computer, only one good enough to beat a certain fidelity threshold.
- High-Fidelity Hardware: The experiment benefited from Quantinuum’s H1-1 ion-trap system, known for its exceptional gate fidelity and all-to-all connectivity. Two-qubit gate fidelities were around 99.94% , which is among the best in the industry. The researchers noted that even a few years ago, no available quantum hardware could have pulled this off. It was the combination of a cutting-edge device and new theoretical insights that made the experiment possible now. The machine’s ability to entangle arbitrary pairs of qubits on demand allowed the 12-qubit circuit to be executed with relative efficiency.
- No “Fine Print” Surprises: Because the authors introduce a new term (quantum information supremacy) with stricter standards, they took care to acknowledge and eliminate potential loopholes. For instance, one could ask: did the quantum device somehow know Bob’s measurement choice in advance (since both were set up on the same hardware) and cheat? The team addressed this by physically separating the processes of random number generation and state preparation, and by planning future setups where Bob’s choice is generated only after Alice’s state is prepared, to mimic true one-way timing. Another possible loophole is whether the ion-trap device truly realized a 12-qubit quantum system, as opposed to some larger effectively classical system. The authors discuss this “hidden space” skepticism – the idea that maybe what looks like a highly entangled state is secretly just a low-dimensional state embedded in a larger space – and argue that pushing to larger separations (more qubits vs exponentially more bits) will further shut down such interpretations. In short, they were transparent about the remaining assumptions and how to address them, giving the result a high degree of integrity.
Taken together, these measures make the result especially credible. It’s not an anecdotal speedup or an artifact of unverified models; it’s a reproducible, statistically significant separation grounded in both physics and theoretical computer science. The study effectively raises the bar for claiming quantum advantage.
Does This Bring Us Closer to Q-Day?
Whenever quantum supremacy is mentioned, a natural question is: does this mean quantum computers can now break encryption or threaten classical cryptography (so-called “Q-Day”)? The short answer is no – not directly. This experiment does not implement Shor’s algorithm or any factorization/cryptanalysis task, so it does not pose a new threat to RSA, ECC, or other current cryptographic systems. The demonstrated quantum advantage is in a very specialized communication/memory task that, while fundamental, is not itself a practical attack on real-world cryptography. It showcases quantum computing’s potential power rather than delivering a useful application (malicious or otherwise) today.
In fact, the authors and commentators emphasize that this result is a proof-of-principle — it “has no immediate commercial application” and doesn’t solve useful problems yet. Instead, its importance is scientific: it confirms that quantum mechanics’ exponential scaling can translate into actual computing advantages in the lab, free from conjecture.
That said, indirect implications for security do exist. Every time a quantum device exceeds classical capabilities, it underscores that the theoretical power of quantum computing is real, not just a mathematical curiosity. This adds weight to the expectation that more directly useful quantum algorithms (like those for breaking cryptography) will eventually become feasible as hardware scales up. In other words, while this experiment doesn’t break any codes, it reaffirms the urgency of developing post-quantum cryptography in the long term. It’s a reminder that we are steadily ticking toward the day when quantum computers are capable of threatening classical encryption – even if that day is not here yet.
In summary, the current work doesn’t change threat models overnight: your encrypted messages are no less safe today than they were before. But it invalidates the skeptic’s safety blanket that “maybe quantum computers will never really outperform classical ones in any clear way.” They clearly can and have now, in a formally unassailable manner. Thus, efforts to transition to quantum-resistant cryptographic schemes (ahead of Q-Day) remain prudent, since the foundational assumption behind them – that quantum machines are fundamentally more powerful on certain problems – has just received its strongest experimental confirmation yet.
Hilbert Space Becomes Reality
Beyond the technical specifics, this milestone speaks to a deeper point about the nature of reality. Quantum computing has long tantalized us with the idea of the Hilbert space of a quantum system – an exponentially large space of possible states that grows as $$2^n$$ for n qubits. For decades, people have asked: Is Hilbert space just an abstract mathematical construction, or do those exponential possibilities truly exist physically? Skeptics speculated that some hidden principle or decoherence might prevent quantum systems from ever fully using that colossal space, meaning quantum computers might never live up to their exponential promise. This experiment provides the most direct evidence yet that Hilbert space is indeed a physical resource that quantum devices can tap into. By showing 12 qubits outmaneuver hundreds of classical bits, the researchers have essentially probed the exponentiality of quantum mechanics and found it working in our universe.
The result is a profound vindication of quantum theory. It says that even in today’s imperfect hardware, we can create and manipulate highly entangled states that live in a space far beyond the reach of any classical description of similar size. The long-running claim that “maybe quantum processors are secretly just classical systems in disguise” is now much harder to support. As the authors write, currently existing quantum processors have demonstrated the ability to “generate and manipulate entangled states of sufficient complexity to access the exponentiality of Hilbert space” – a poetic way of saying the quantum world’s extra dimensions of possibility are real and usable. It’s a reminder that when we harness even a handful of qubits, we are leveraging an almost otherworldly richness of nature’s information capacity, one that defies our classical intuitions.
Quantum Upside & Quantum Risk - Handled
My company - Applied Quantum - helps governments, enterprises, and investors prepare for both the upside and the risk of quantum technologies. We deliver concise board and investor briefings; demystify quantum computing, sensing, and communications; craft national and corporate strategies to capture advantage; and turn plans into delivery. We help you mitigate the cquantum risk by executing crypto‑inventory, crypto‑agility implementation, PQC migration, and broader defenses against the quantum threat. We run vendor due diligence, proof‑of‑value pilots, standards and policy alignment, workforce training, and procurement support, then oversee implementation across your organization. Contact me if you want help.