New Paper Alert: Brace for Impact: New ECDLP Challenge Ladder Benchmarks Quantum Threat to Bitcoin
August 2025 – A team of researchers has unveiled a new cryptographic challenge suite designed to track the advance of quantum computers toward breaking Bitcoin’s encryption. In a paper titled “Brace for impact: ECDLP challenges for quantum cryptanalysis,” Pierre-Luc Dallaire-Demers and colleagues introduce a difficulty-graded ladder of elliptic curve discrete logarithm (ECDLP) problems based on Bitcoin’s secp256k1 curve. The ladder spans from a toy 6-bit prime-field instance up to the full 256-bit secp256k1 cryptosystem used in Bitcoin, providing a “transparent, fine-grained ruler” to benchmark the progress of fault-tolerant quantum computers (FTQCs) running Shor’s algorithm.
This development addresses a notable gap in cryptographic benchmarks: while factoring challenges have long existed for RSA, the ECDLP (used in elliptic-curve cryptography) lacked an adequate, incrementally scaled set of public challenges.
Each rung of the new ECDLP challenge ladder is calibrated against both classical and quantum metrics. The authors anchor the difficulty of these elliptic-curve puzzles to known classical attack records (Pollard’s rho algorithm) and then estimate the quantum resources needed to solve them via Shor’s algorithm. By compiling Shor’s ECDLP circuit for each challenge size and mapping it to different error-corrected quantum hardware models, they produce concrete targets for qubit counts and runtimes. The headline finding: a cryptographically relevant quantum computer might crack Bitcoin’s 256-bit curve if it can marshal on the order of 105-106 high-quality qubits, potentially as soon as the 2027-2033 timeframe under optimistic assumptions. This sobering timeline – just a few years away – underscores the authors’ call for urgent migration of digital assets to post-quantum safe cryptography.
Filling the Benchmark Gap: Canaries for Quantum Cryptanalysis
Modern cryptocurrencies and secure communications rely on problems like ECDLP remaining intractable to classical computers. Unlike the well-known RSA factoring challenges, however, elliptic-curve systems have lacked a fine-grained public benchmark to measure year-over-year cryptanalytic progress. Prior elliptic-curve challenges were either too sparse (e.g. the 2009 Certicom ECC challenges) or not directly representative of a full discrete log attack. For example, the so-called “Bitcoin puzzle” addresses and recent Proof-of-Quantum challenges constrained the secret key to a smaller interval, making those puzzles solvable with specialized algorithms (Pollard’s kangaroo) rather than a true full-range discrete log attack. In short, the community has “needed simple, public, reproducible rulers” to track how close quantum computers are to breaching real-world elliptic-curve crypto.
To meet this need, Dallaire-Demers et al. propose the new ECDLP challenge ladder as an early warning system – “canaries” for the quantum era. The ladder provides a sequence of standardized ECDLP instances that can signal quantum milestones: if a future quantum computer (or any algorithmic breakthrough) conquers a higher-bit challenge that was previously infeasible, that success flags a tangible leap in cryptanalytic capability. “Imperfect” as any single benchmark may be, the authors argue these challenges are “still the best early warning we can maintain and audit” for the approach of quantum threat levels. Notably, no group has yet demonstrated Shor’s algorithm end-to-end on any elliptic curve problem in the lab – but hardware trends suggest the first such feats “may be close”. By introducing an entire ladder now, the researchers aim to have a yardstick in place before those breakthroughs occur, to monitor and compare progress in a public, transparent way.
Ladder of Bitcoin’s Curve: From 6 Bits to 256 Bits
At the core of the paper is a deterministic, reproducible recipe for generating elliptic-curve challenge instances that look just like Bitcoin’s secp256k1, only scaled down in prime size. Bitcoin’s secp256k1 uses a 256-bit prime modulus for its finite field; the challenge ladder keeps the exact same curve equation (y² = x³ + 7 over prime p) and base point structure, but varies p from 256 bits all the way down to a toy 6-bit prime. For each target size k in {6, 7, 8, …, 256} bits, the authors provide the curve’s prime p, a base point Gp, and a sample public key Q = d·Gp – the challenge is to solve for the discrete log d. All these parameters are generated in a deterministic way (with published code), ensuring anyone can independently reproduce the exact same challenges. In essence, they have created scaled-down “mini-Bitcoin” curves – dubbed secpk1 for various bit-lengths – that preserve the mathematical structure of the real thing while offering progressively easier problems for testing purposes.
Crucially, the difficulty progression is fine-grained. A 6-bit prime field ECDLP is laughably easy for classical computing – one can solve it by hand or brute force in milliseconds. (Indeed, the 6-bit challenge can be solved by hand by a motivated reader.) But implementing Shor’s algorithm to solve even this trivial instance on a fault-tolerant quantum computer would be a significant milestone, requiring a full stack of error-corrected operations.
From there, the challenges tick upward in size – 8-bit, 10-bit, 16-bit, 32-bit, and so on – bridging the huge gulf between today’s tiny quantum demonstrations and the 256-bit security of Bitcoin. The largest rung, naturally, is the full 256-bit secp256k1 ECDLP itself. Notably, the authors selected as the 256-bit target a particularly famous instance: the public key from Bitcoin’s genesis block (the very first Bitcoin address, an unspendable coinbase output). While no one can spend those particular 50 BTC by design, using the genesis public key as the challenge makes the problem deeply concrete – cracking it would be synonymous with shattering Bitcoin’s original cryptographic security. Together, this ladder of challenges offers a continuous scale to measure progress, rather than a few disparate data points. It serves as “a transparent, fine-grained ruler for both classical and fault-tolerant quantum progress” on ECDLP, as well as “a concrete impetus to migrate digital assets to post-quantum signatures” before the highest rungs come within reach.
On the classical side, the authors calibrate the ladder against known results to give it real-world meaning. The difficulty of generic ECDLP scales roughly as O(2n/2) for an n-bit curve (Pollard’s rho algorithm being the best known generic attack). In practice, the largest publicly solved ECDLP instances to date are on the order of ~112-113 bits, achieved through massive distributed computing efforts. For example, a 112-bit prime-field ECDLP was solved using thousands of PlayStation 3 consoles working in concert , and a 113-bit binary-field ECDLP was cracked on a specialized FPGA cluster. (By comparison, Bitcoin’s 256-bit keys are astronomically out of reach for classical brute force.)
The new challenge suite deliberately includes mid-sized instances around the 100+ bit level to align with those historical records. This provides a calibrated classical baseline – if a team attempts a 112-bit secp challenge, classical Pollard-rho should require on the order of 256 operations, consistent with prior results. By anchoring to published records, any speedups or breakthroughs can be measured as clear deviations from the expected curve.
The ladder design also distinguishes full-range ECDLP challenges from easier interval-restricted ones: unlike the “Bitcoin puzzle” challenges where the private key was intentionally small (making Pollard’s kangaroo algorithm viable), these ladder instances assume a full 256-bit range for the secret, necessitating the true periodic structure that only Shor’s algorithm (or generic rho) exploits. In short, the authors have set the stage so that success on each challenge rung equates to meaningful cryptanalytic progress, either through classical ingenuity or, more likely, quantum computing power.
Quantum Resource Estimation and the Road to a 256-bit Break
The technical tour de force of the paper lies in mapping Shor’s algorithm for ECDLP onto concrete quantum hardware models, from logical circuit counts down to physical qubit requirements. For each challenge size, the team uses a detailed logical cost model for Shor’s algorithm – including the number of logical qubits needed, the depth of the quantum circuit, and the count of non-Clifford gates (like T gates/Toffolis which drive much of the error-correction overhead). These logical resource counts were obtained using tools like Microsoft’s Quantum Resource Estimator, exploring various optimization trade-offs (low-depth vs. low-qubit vs. low-T implementations). Tables in the paper enumerate, for example, that a 256-bit ECDLP might require on the order of 50 million T gates and 100+ logical qubits in an optimized construction – staggering numbers by today’s standards, but within the realm of what error-corrected quantum architectures could tackle with large-scale hardware.
The next step is translating those logical requirements into physical hardware demands under different quantum error-correction codes. The authors consider several leading approaches: the conventional surface code (a 2D grid of qubits with topological error correction), as well as emerging high-efficiency designs like the repetition cat code and LDPC cat codes (being pursued by companies like Alice&Bob) which promise to trade more complex qubit encodings for lower overhead. By running simulations and formulae for each approach, they estimate how many physical qubits and how much runtime would be needed to execute Shor’s algorithm for a given ECDLP size in a fault-tolerant manner.
The results are sobering but also illuminating. In a conservative scenario using surface codes with modest error rates, a full 256-bit discrete log might require on the order of millions of physical qubits, and could take many hours or days to run. This essentially reinforces that today’s quantum machines (with 100(s) of noisy qubits) are nowhere near the threat level – but it sets a quantitative bar for the future.
In a more optimistic scenario – using an aggressive combination of techniques like faster cycle times, efficient magic-state factories, and the latest cat-code improvements – the resource burden drops dramatically. The paper cites recent breakthroughs that brought the estimated cost of breaking ECC-256 down to ~126,000 qubits with a 9-hour runtime (using a bias-preserving cat code architecture).
Further optimizations in 2023-2025 (e.g. magic-state cultivation and more efficient period-finding algorithms) have continued to chip away at the requirements.
Under the most aggressive assumptions outlined, the authors project that “a few × 104” physical qubits might suffice to crack secp256k1 in under a day – a startling figure that, if achieved, would put Bitcoin’s signature scheme firmly in the crosshairs of a quantum adversary.
To put these numbers in context, the team juxtaposed their cryptanalysis resource estimates with the public roadmaps of quantum hardware vendors. Tech giants and startups alike have announced plans for scaling qubit counts into the hundreds of thousands or even millions within the next decade. IBM’s latest roadmap aims for >100,000 qubits by 2033; IonQ has projected reaching #2 million# qubits by 2030 in investor materials; other players like Google, Quantinuum, Pasqal and Alice&Bob likewise have bold goals. While such claims are aspirational, they indicate that the necessary scale of hardware could arrive in the 2027-2033 window if progress continues unabated. The authors compiled a timeline chart (their Figure 5) overlaying the algorithmic milestones – e.g. the qubit requirements to break RSA-2048 and ECC-256 – against these hardware progress trajectories to identify when they intersect.
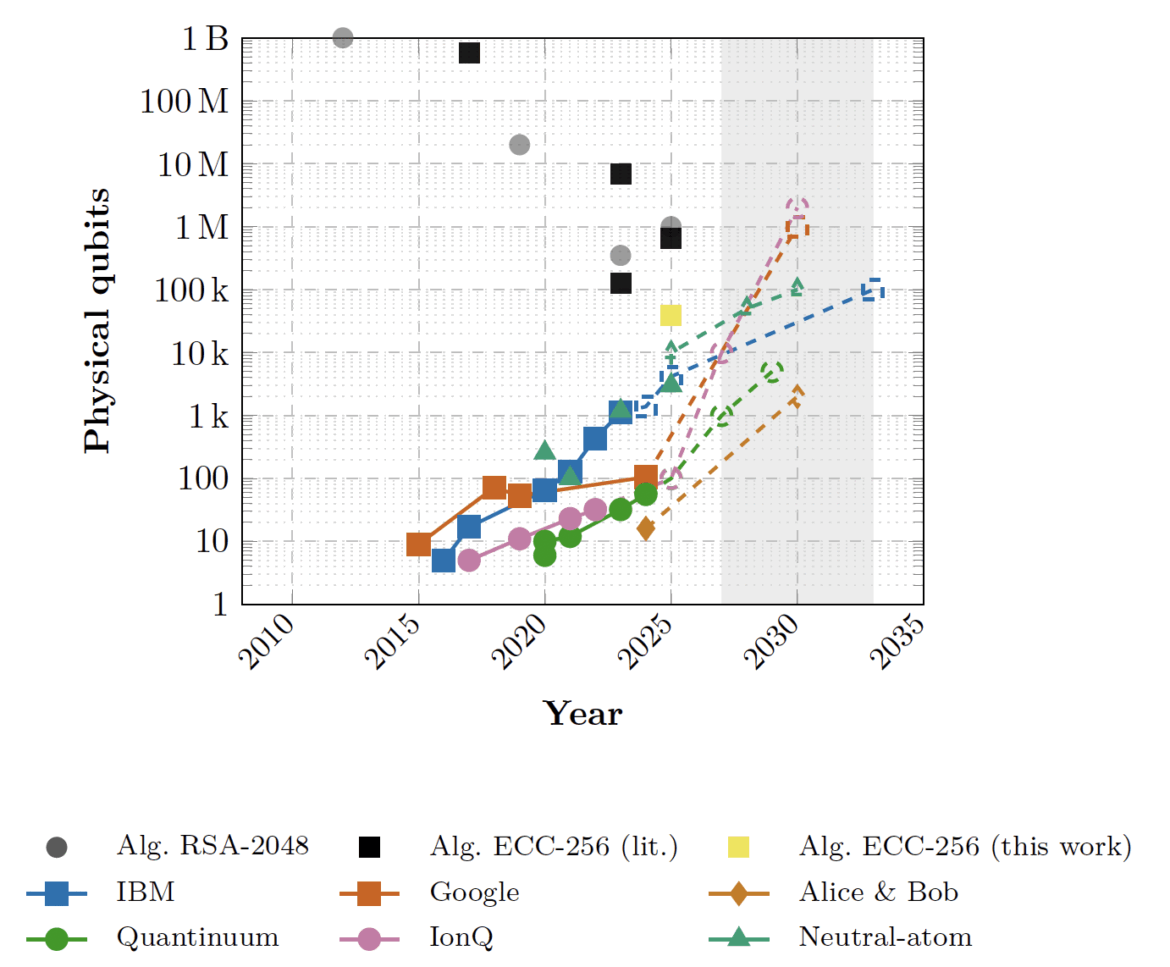
Figure: The researchers’ “forecast” overlay plots quantum cryptanalysis resource requirements versus industry hardware roadmaps. In this log-log chart (adapted from Figure 5 of the paper), algorithmic breakthroughs are marked as black/gray squares and circles (for ECC-256 and RSA-2048), while colored dashed lines trace projected qubit counts from major quantum hardware efforts (IBM, Google, Quantinuum, IonQ, etc.). The shaded band indicates the first plausible collision between quantum capability and the ECDLP challenge – roughly in the 2027-2033 timeframe where the hardware lines cross the ECC-256 threshold.
This visualization suggests that, if quantum engineering advances continue on their current curve, the late 2020s to early 2030s could witness a quantum computer powerful enough to jeopardize 256-bit secp256k1. The authors emphasize that this is not a precise prediction but a “calibrated overlay” of today’s best data. The timeline could shift sooner with unexpected breakthroughs, or later if technical hurdles (the “three levers” of magic-state supply, error-correcting code distance, and classical control latency) prove harder to overcome. Nevertheless, the takeaway is clear: on our current trajectory, we may only be a handful of years away from quantum machines that put Bitcoin and similar elliptic-curve systems at risk.
With this in mind, the paper drives home the need for proactive migration to post-quantum cryptography. Waiting until a quantum computer is actually demonstrated solving a 256-bit ECDLP would be waiting too long. The authors urge the community not to treat the 2027-2033 window as distant science fiction, but as an imminent horizon for which preparations must begin now . By quantifying the threat in testable terms – qubits, gate counts, and years – their ECDLP challenge ladder provides a concrete yardstick against which to measure our remaining safe time to upgrade cryptographic protections.
Analysis: A Quantum Benchmark with Broad Security Implications
Beyond its technical contributions, this ECDLP challenge suite arrives as an important tool for the quantum risk management and cryptographic migration community. It effectively translates the abstract threat of quantum computing into a series of measurable milestones. Security leaders and crypto asset custodians have been asking: “How will we know – and when will we know – that quantum computers are catching up to our cryptography?” These new benchmarks offer a tangible way to answer that. As the authors note, a graded challenge ladder can act as an early warning system – a set of “public, reproducible rulers” that the community can monitor. Each time quantum hardware ticks up to conquer the next ECDLP rung (say 100-bit, 150-bit, 200-bit), it will send a clear signal that the threat to 256-bit keys is moving from theoretical to practical. Such signals are invaluable for risk managers developing migration roadmaps: they provide a quantifiable trigger point to start or accelerate the transition of vulnerable systems to post-quantum algorithms.
In short, the ladder makes the quantum threat trajectory auditable. It replaces vague predictions with concrete data points – something businesses and governments can use in planning exercises and policy decisions.
Equally novel is the choice of Bitcoin’s secp256k1 curve as the universal benchmark. By using the actual curve securing hundreds of billions of dollars in cryptocurrency, the challenges ensure that progress in the lab translates to real-world impact. This is a departure from past cryptographic challenges, which often used toy problems or unrelated hard instances. Here, any breakthrough on the ladder immediately answers “Could it crack Bitcoin (or Ethereum, etc.) if scaled up?” in a directly relevant way. This focus on an economically significant curve is likely to galvanize attention. It creates a common target for interdisciplinary efforts – cryptographers, quantum algorithm designers, and hardware engineers can all rally around the same problem. The authors explicitly designed the suite to be a “shared language” for communities that “rarely speak together”, from theoretical algorithm designers to experimental quantum labs. Now, an optimization in a quantum algorithm can be measured by how many bits it shaves off the ECDLP requirement, or a hardware improvement by which challenge size it enables – a unifying metric that transcends specialties. This could foster healthy competition too: academic groups, national labs, or companies might start racing to climb the ladder (much as past generations raced to factor bigger RSA numbers), each successively demonstrating “we’ve solved secp*k1 at X bits.” Such reproducible achievements will build a track record that keeps the wider community informed of where we stand on the path to full 256-bit quantum cryptanalysis.
Finally, the introduction of this public challenge suite has strategic and policy implications for several stakeholders in the digital asset and security ecosystem:
- Crypto Asset Custodians (Exchanges, Wallet Providers, Institutions): For those holding or safeguarding cryptocurrencies, the ladder’s timeline concretizes quantum risk. It encourages custodians to re-evaluate how long their elliptic-curve-based keys can remain safe. With a plausible quantum break-in window of 2027-2033 now on the radar , custodial services should begin migrating customer funds to quantum-resistant addresses or implement contingency plans (such as key rotation schemes or hybrid multi-signatures). The challenge results will let them track quantum capability closely – for example, if a 128-bit ECDLP is cracked in 2025, that might be a cue to accelerate migrating any remaining exposed 256-bit keys. In essence, this benchmark provides a more empirical basis for quantum risk management, turning it from a theoretical worry into a series of milestones with dates attached.
- Bitcoin Core Developers & Crypto Protocol Designers: The fact that secp256k1 itself is used as the benchmark sends a strong message to protocol developers. Up to now, discussions about upgrading Bitcoin or other blockchains with post-quantum signature schemes have been largely academic, often met with inertia due to implementation challenges and uncertainty about the threat timeline. Now, however, the clock is ticking in a visible way. The paper’s authors explicitly “motivate proactive migration” to post-quantum signatures – and provide the data to justify it. Bitcoin developers and the broader community can use the challenge ladder as a decision-making tool: if quantum efforts reach, say, the 160-bit or 192-bit ECDLP level, it would be hard to argue against moving forward with a PQC upgrade (such as introducing new address types or soft-forking in a quantum-safe signature option). By framing quantum readiness in terms of Bitcoin’s own security parameters, the challenge suite effectively puts the issue on the agenda with greater urgency. It helps build consensus by showing when the threat becomes not just possible but palpable, ideally spurring preemptive action rather than reactive panic.
- Quantum Computing & Security Researchers: For the research community, these ECDLP challenges establish a clear, reproducible benchmark for progress in quantum cryptanalysis. They will likely become a reference point in academic papers and industry reports: e.g., “our new qubit architecture solved the 30-bit secp challenge” or “our algorithmic improvement saves 20% of the qubits required for the 256-bit instance.” This encourages researchers to focus on economically meaningful targets (breaking widely used crypto) instead of abstract metrics. It also levels the playing field for evaluating different quantum approaches – one can compare a superconducting platform to an ion-trap platform by seeing which secp*k1 challenge each can tackle, providing an apples-to-apples metric for cryptanalytic performance. In broader terms, the ladder can guide funding and policy priorities in quantum research: it outlines intermediate goals (like 128-bit, 192-bit ECDLP) that agencies and companies might set in roadmaps as stepping stones to the ultimate objective of defeating 256-bit ECC. By making those goals explicit and trackable, the community can better coordinate its efforts and measure returns on investment in quantum technologies. And as a public challenge, it invites independent validation – any breakthrough claimed can be checked by others using the published parameters, which is crucial for a field where extraordinary claims will need clear proof.
Conclusion
The “Brace for Impact” ECDLP challenge suite is a great attempt to translate a looming cryptographic crisis into a concrete set of problems we can grapple with today. It provides a much-needed “ruler” to measure where we stand in the race between encryption and quantum decryption. The choice of Bitcoin’s secp256k1 curve for these challenges ties the abstract math to real economic stakes, lending a sense of urgency (and opportunity) to everyone from Bitcoin developers to national security planners. Most importantly, it empowers the community with an actionable early warning system: as soon as a quantum computer ticks up the ladder, we will know, undeniably, that the time has come to brace for impact and switch our cryptography to higher ground.
