Neutral Atoms Cross a Fault-Tolerance Milestone – This Time With Logical Control
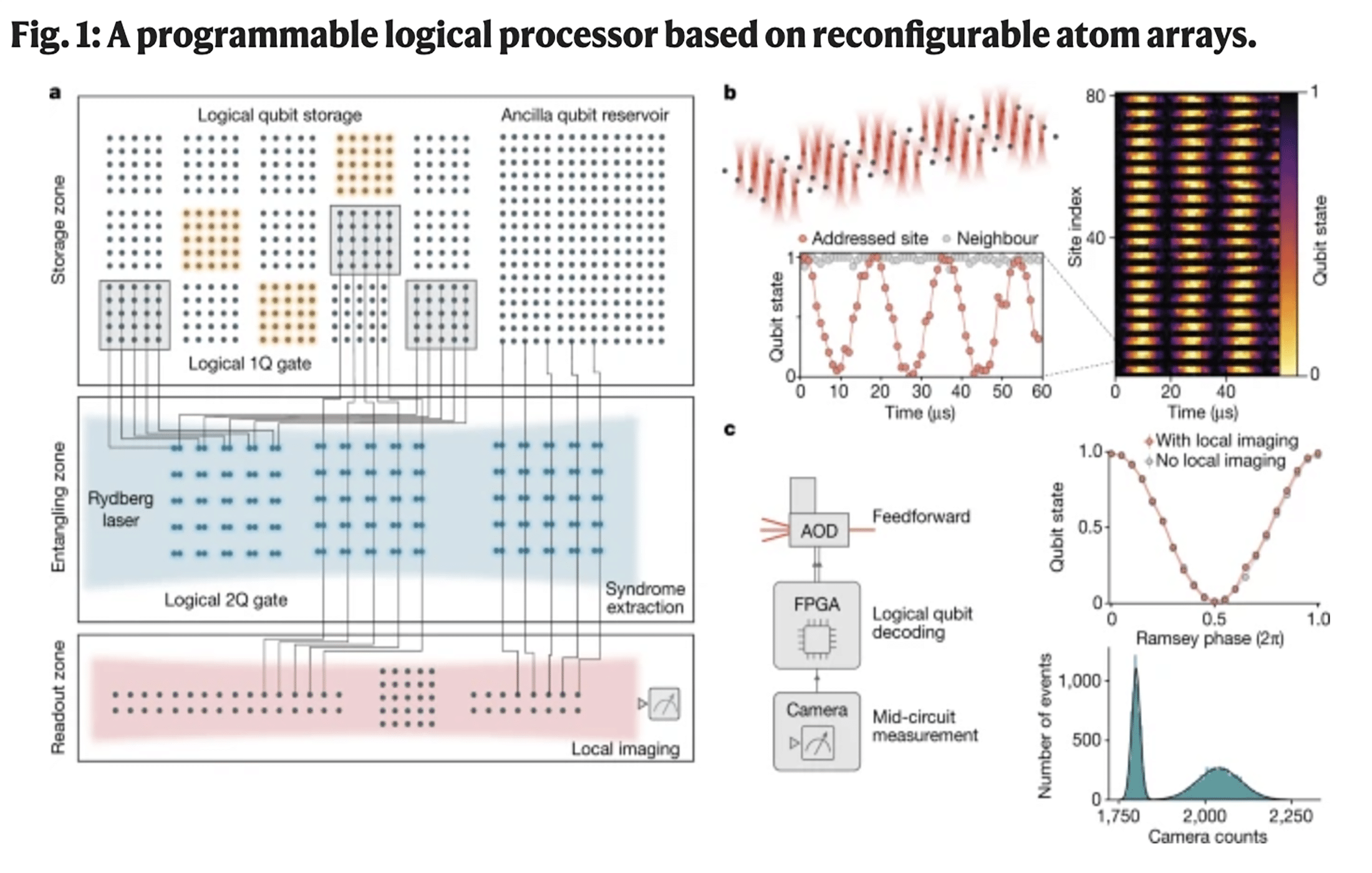
Table of Contents
News Summary
Dec 2023 – The Harvard-MIT-QuEra team led by Mikhail Lukin published what I consider one of the most consequential neutral‑atom results to date: a programmable logical quantum processor that uses reconfigurable arrays of rubidium atoms to execute error‑corrected circuits at the logical level, with performance that improves as code distance increases and with clear, measured algorithmic benefits from encoding. The paper appeared in Nature on December 6 (open access): “Logical quantum processor based on reconfigurable atom arrays,” Evered, Bluvstein, Kalinowski, et al. DOI: 10.1038/s41586‑023‑06927‑3.
The news, in brief
- Platform: A reconfigurable array of up to 280 laser‑trapped $$^{87}$$Rb atoms. The system separates storage, entangling, and readout into three physical zones; qubits are moved between zones during the circuit. Connectivity comes from physically interlacing atom grids and applying a global Rydberg entangling pulse. Figure 1 on page 59 sketches the architecture and shows mid‑circuit readout (≈99.8% fidelity over 500 µs imaging, with negligible effect on data‑qubit coherence).
- Control at the logical level: Instead of programming every physical qubit line‑by‑line, they issue block‑wise logical operations (e.g., transversal single‑qubit rotations via frequency‑multiplexed AOD beams). That multiplexing is why this scales on atom arrays.
- Surface‑code entangling gate that gets better with distance: They implement a transversal CNOT between two surface codes and measure a decrease in Bell‑pair error as the code distance increases from d = 3 to 5 to 7, provided you decode using the correlations that arise during transversal gates (“correlated decoding”). For d = 7 they measure ≈0.95 populations in both XX and ZZ logical bases (see Fig. 2, page 60), and the Bell‑pair error vs distance curve shows the improvement.
- “Break‑even” in state preparation (colour code): Using d = 3 colour codes and a flagged, fault‑tolerant init circuit, they report logical |0⟩ initialization fidelity of 99.91%, exceeding both the best physical |0⟩ init (99.32%) and their physical two‑qubit gate fidelity (~99.5%). That’s a break‑even result for SPAM fidelity at the logical level. (Fig. 3b, page 61.) They then create a 4‑logical‑qubit GHZ state with 72(2)% fidelity – rising to 99.85+0.1/−1.0% with post‑selected error detection. (Fig. 3c-e.)
- Mid‑circuit feedforward at the logical level: They demonstrate entanglement teleportation with a mid‑circuit logical measurement and conditional S gates, reaching 77(2)% Bell fidelity (or 92(2)% under error detection). (Fig. 4d-e, page 62.)
- Classically hard circuits with non‑Cliffords using 3D [[8,3,2]] codes: By switching to small 3D codes that admit transversal CCZ, they run IQP‑type sampling circuits on 48 logical qubits (hyper‑cube connectivity), applying 228 logical two‑qubit gates + 48 logical CCZ. The logical XEB score is finite across sizes and reaches ≈0.1 at 48 logical qubits – well above what they (and I) would expect from a physical‑qubit implementation at the same scale. (Fig. 5e-f, page 63.)
- Numbers to bookmark: Two‑qubit Rydberg‑gate fidelities 99.3-99.5% (Methods); mid‑circuit imaging fidelity ≈99.8% (Fig. 1c); and a forward path outlined to >10,000 physical qubits by boosting laser power and refining controls, with a target of 0.1% two‑qubit errors. (Outlook, page 64.)
What they actually achieved (and what they didn’t), in plain terms
1. Error suppression with scaling – on a neutral‑atom platform.
The result everyone should internalize: when they scale a surface code from d = 3 to d = 7, the logical entangling operation improves. In other words, the curve bends the right way – performance increases with code distance, a hallmark of being below an effective threshold for the circuit they executed. The improvement depends on decoding across the two codes (because a transversal CNOT deterministically propagates certain errors), which they handle with a correlated hypergraph decoder (Fig. 2b-d; Methods). That’s the key experimental insight.
(Caveat: this is not repeated, round‑by‑round surface‑code error correction. They perform one round of syndrome extraction and then a projective readout; for true fault‑tolerant operation over deep circuits you’d repeat noisy syndrome extraction many times, which carries a lower threshold. They say so explicitly and list it as “an important goal for future research.” )
2. “Break‑even” precisely defined.
I’ve seen people equate this paper with a “logical lifetime exceeds best physical lifetime” milestone. That’s not what’s shown here. The specific break‑even they claim – and demonstrate – is logical state‑prep fidelity exceeding their best physical state‑prep and two‑qubit gate fidelities, for a d = 3 colour code. That’s a meaningful and carefully scoped claim. There is no claim of a logical T₁/T₂ lifetime beating the best physical qubits, nor of repeated‑cycle surface‑code break‑even. (Fig. 3b, page 61.)
3. Real, programmable logical algorithms.
Everything after Figure 3 is a reminder that encoding is not a hobbyist feature – it improves algorithmic performance in ways you can measure. The XEB of their 12‑logical‑qubit IQP circuit rises from 0.156(2) to 0.616(7) with logical error detection; for 48 logical qubits, the XEB ≈ 0.1 after hundreds of entangling gates. They also show two‑copy measurements of entanglement growth (a Page‑curve signature) and quantify additive Bell magic as they increase the number of logical CCZs. (Fig. 5 & Fig. 6, pages 62-64.)
4. Engineering wins that matter for scale.
A lot of the heavy lifting is systems work: AOD‑based frequency‑multiplexed control to address many sites with just a couple of analog waveforms; high‑fidelity local single‑qubit gates; fast atom transport; and mid‑circuit readout/FPGA feedforward in ≲1 ms. (See Fig. 1, Extended Data Figs. 1-3, Methods.) This is how you reduce classical control overhead as codes grow.
How I read the significance
- Neutral atoms join superconductors and ions at the logical table. We’ve had beautiful logical demos from trapped ions and superconducting qubits; this paper shows neutral‑atom arrays can play the same game – and exploit unique strengths: flexible non‑local connectivity via transport and a natural fit for block‑wise, transversal gates. That’s strategically important for architectures where routing dominates cost.
- Two complementary stories in one machine:
- Surface‑code scaling of a transversal entangling gate (Clifford land), where they show distance‑dependent suppression.
- 3D‑code sampling with CCZ (non‑Clifford land), where encoding boosts algorithmic fidelity beyond what their physical gates can support at the same depth/connectivity. That second story is a use‑case‑driven path to early, error‑detected advantage.
- Postselection is a tool, not a crutch. The team is transparent: many of the headline fidelities use sliding‑scale error detection (postselection). That trades throughput for sample quality – often the right trade when the goal is to show how encoding moves you up the fidelity curve and to probe physics like scrambling/magic (Fig. 3d, Fig. 5e). The next step is clear: repeat syndrome extraction during algorithms to reduce reliance on postselection.
What to watch next (and what would convince me we’re ready for large‑scale FTQC)
- Repeat syndrome extraction during logic (e.g., many rounds of noisy surface‑code cycles wrapped around transversal gates) to show below‑threshold operation without postselection. The authors point to this explicitly as the “key future milestone.”
- Drive two‑qubit errors from ~0.5-0.7% to ~0.1% (their target) and show the expected exponential suppression with distance in more complex circuits.
- Tighten the full stack – faster mid‑circuit readout, zone‑specific Raman controls to cut idling decoherence (they estimate ~1% logic decoherence per extra encoding step today), and continuous atom reload from reservoirs for deep circuits. (Fig. 4c, Outlook.)
- Non‑Clifford at scale with lower overhead. Their use of [[8,3,2]] is a smart code-algorithm co‑design trick for CCZ. Long term, watch for magic‑state factories or code switching on neutral atoms as the two‑qubit fidelity improves.
Why this matters for security & PQC timelines
This doesn’t move RSA‑2048 into the “next few years” bucket. What it does change is my confidence in neutral‑atom arrays as a credible path to big, error‑corrected machines. The ability to improve an entangling logical operation by increasing distance, to execute non‑Clifford logical circuits at scale, and to show measurable algorithmic benefits from encoding – all on a platform that can, in principle, reconfigure connectivity on the fly – reduces execution risk on the long road to factoring‑class fault tolerance. For PQC decision‑makers, this is another nudge to finish the migration rather than wait for uncertainty to resolve itself.
Quantum Upside & Quantum Risk - Handled
My company - Applied Quantum - helps governments, enterprises, and investors prepare for both the upside and the risk of quantum technologies. We deliver concise board and investor briefings; demystify quantum computing, sensing, and communications; craft national and corporate strategies to capture advantage; and turn plans into delivery. We help you mitigate the cquantum risk by executing crypto‑inventory, crypto‑agility implementation, PQC migration, and broader defenses against the quantum threat. We run vendor due diligence, proof‑of‑value pilots, standards and policy alignment, workforce training, and procurement support, then oversee implementation across your organization. Contact me if you want help.



