New Paper Alert: “Low‑Overhead Transversal Fault Tolerance for Universal Quantum Computation”
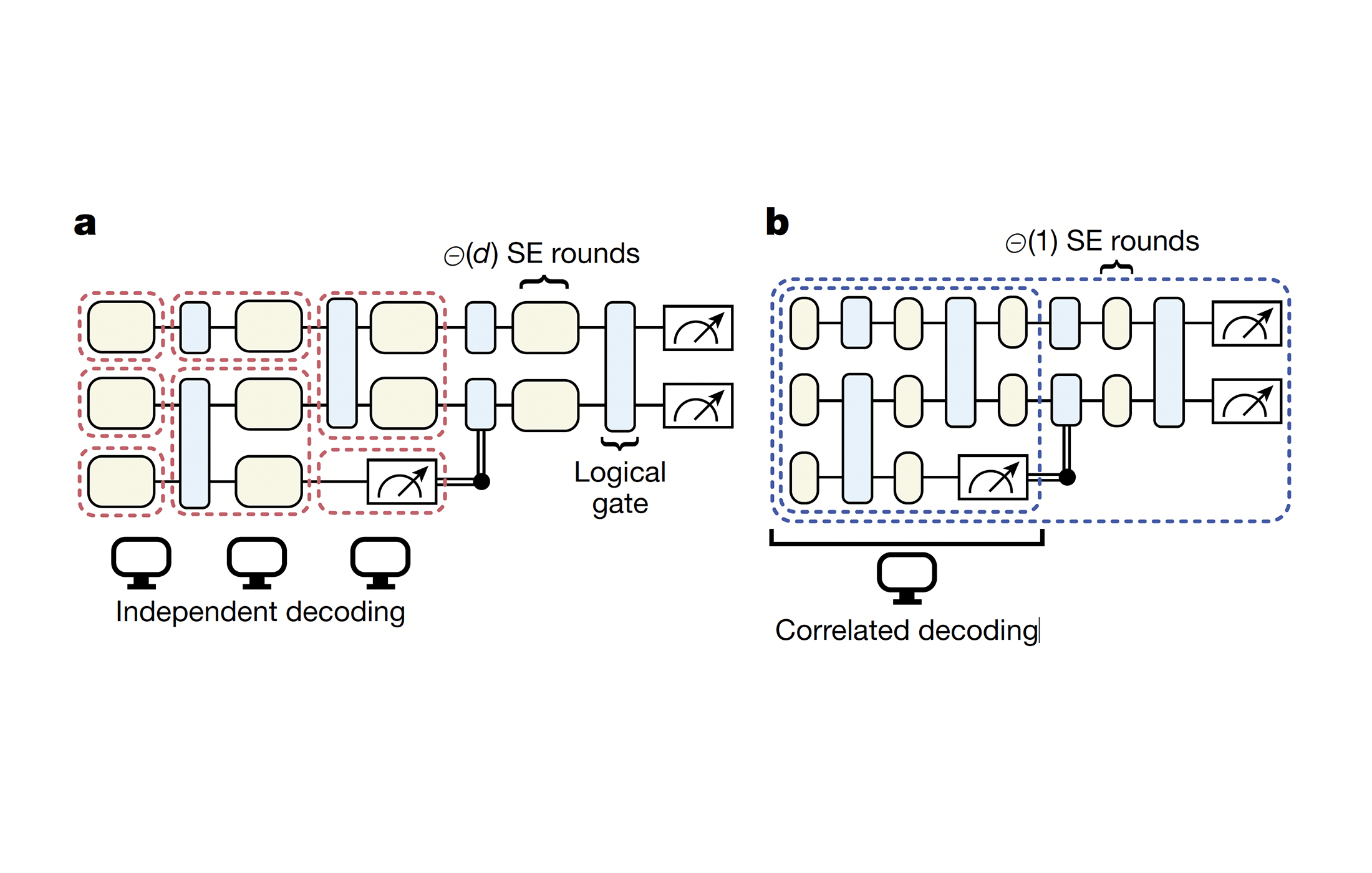
Table of Contents
24 Sep 2025 – A new fault-tolerance framework unveiled by researchers from QuEra, Harvard, and Yale promises to drastically reduce the time overhead of quantum error correction. Published yesterday in Nature as “Low‑Overhead Transversal Fault Tolerance for Universal Quantum Computation” (Zhou et al., 2025), their method – called Transversal Algorithmic Fault Tolerance (AFT) – eliminates the usual slowdown from repeated error-checking cycles.
By cutting this overhead by an order of magnitude, the breakthrough could accelerate the arrival of cryptanalytically relevant quantum computers (CRQCs) capable of breaking classical encryption. In short, quantum algorithms (like Shor’s factoring) might run 10-100× faster under this scheme, shrinking the timeline for when today’s cryptography could be at risk.
(As always with such cutting edge research, I don’t want to make definitive statements – this approach could potentially accelerate Q-Day timelines, contingent on hardware scaling and decoder performance. It’s not guaranteed, but it is plausible and significant.)
Executive Summary
What was achieved? The AFT framework shows that a wide range of quantum error-correcting codes – including the popular surface code – can perform fault-tolerant logical operations with only a constant number of syndrome extraction rounds, instead of the typical $$d$$ rounds (where d is the code distance).
In practical terms, this means error-corrected quantum gates no longer need to be slowed down by repeated error-check cycles proportional to d. The team demonstrated that even with far fewer checks, the probability of a logical error still drops exponentially with d, preserving reliability. This dramatically speeds up quantum computations without sacrificing error suppression.
How did they do it? AFT combines two key ideas in a novel way:
- Transversal operations: Apply the same logical gate in parallel across all qubits in an encoded block. This way, any single physical qubit error stays local and cannot spread throughout the code, making errors easier to detect and correct. Transversal gates are inherently fault-tolerant by design, as a single fault won’t cascade into multi-qubit damage.
- Correlated decoding: Rather than analyzing each error syndrome measurement round in isolation, AFT uses a joint decoder that looks at the combined pattern of all syndrome data up to the point of a logical operation. By correlating these partial clues, the decoder can still correctly infer errors and ensure logical error rates decay exponentially with the code distance d. In essence, the code’s full error-correcting power is realized without needing $d$ rounds of checks upfront.
Why is this important? In standard quantum error correction (e.g. with surface codes), an operation on a logical qubit often requires repeating a syndrome measurement $$d$$ times to ensure any measurement errors don’t induce a logical fault. For a high-reliability algorithm, $$d$$ might be 25, 30, or more – meaning a huge slowdown where each logical gate takes 25-30 cycles of checking. This new framework slashes that overhead to a constant (say 1 or 2 rounds total) per operation. For example, if $$d=30$$, AFT can theoretically make the quantum program ~30× faster by removing 29 extra cycles from every gate.
The Nature paper reports runtime reductions on the order of d (often ~30 in simulations), translating to 10-100× speedups in executing large-scale algorithms when mapped to certain hardware.
Notably, the researchers highlight neutral-atom quantum computers as prime beneficiaries. Neutral-atom arrays use identical atoms as qubits, can be reconfigured on the fly. Furthermore, they do not require the bulky dilution refrigerators necessary for superconducting qubits, simplifying the infrastructure required for scaling. A common concern, however, is their slower gate operations (due to moving atoms or sequential laser pulses). AFT turns this weakness into strength: because neutral atoms can be dynamically rearranged, they support flexible transversal gate layouts that conventional superconducting chips can’t easily do. By needing only one syndrome round per logical layer, the “transversal algorithmic” approach leverages the high connectivity of atom arrays to perform error correction more efficiently.
In fact, QuEra’s team projects 10-100× faster execution of complex algorithms on reconfigurable neutral-atom hardware using AFT. This means that despite slower individual gates, neutral-atom quantum computers could achieve competitive – or even superior – runtime for error-corrected algorithms, all while retaining their advantages in scalability and simple infrastructure.
Implications for CRQC timelines
By sharply reducing the overhead needed for fault tolerance, this approach could bring forward the timeline for a quantum computer that threatens current cryptography.
As a case in point, a companion study applied the AFT framework to Shor’s algorithm (used for factoring large integers) on a neutral-atom architecture. The result: a 2048-bit RSA key could be factored with about 19 million physical qubits in 5.6 days (assuming 1 ms operation cycles). This is roughly 50× faster than prior resource estimates under similar assumptions, which might have envisioned months-long runtimes. In practice, such a reduction means that once million-qubit machines exist, breaking RSA-2048 could potentially drop from a months-long endeavor to under a week – a drastic shift in cryptographic risk.
By cutting time (and keeping the qubit count the same), AFT lowers the barrier for achieving a cryptanalytically relevant quantum computer. Quantum-safe cryptography deployments may need to happen sooner than expected, as this research shortens the horizon on which large-scale fault-tolerant quantum computers become operational.
(In summary, CISOs, CIOs, and policymakers should note: this breakthrough shows a path to much faster error-corrected quantum computing. It could accelerate quantum advantage and the day a quantum computer can break public-key cryptography, underscoring the urgency of moving to post-quantum encryption in the near future.)
Technical Summary: Transversal Fault Tolerance Explained
For readers interested in the technical underpinnings: the crux of AFT is re-imagining fault tolerance at the algorithm level rather than the gadget level, ensuring the final logical output is correct even if intermediate steps are noisy. Key mechanisms include transversal gates, constant-time syndrome extraction, correlated decoding, and the use of CSS quantum codes like the surface code.
Transversal Operations with Constant-Time Error Extraction
“Transversal” operations are a cornerstone of this scheme. An operation is transversal if it applies identical local gates across all qubits of an encoded block simultaneously. Many quantum codes have at least some transversal gates (especially within the Clifford group). For example, a transversal CNOT can be performed between two code blocks by pairing up qubits, and applying CNOTs in parallel – any single error in one pair doesn’t propagate to others. All logical Clifford operations in the AFT protocol are implemented transversally by construction. This ensures that a single physical fault during the operation results in at most one fault in each code block, which the code’s error-correcting capability can handle.
Crucially, AFT limits syndrome extraction (SE) to a constant number of rounds per operation, often just one round immediately following the transversal gate. In each SE round, ancilla qubits are coupled to the data block to measure stabilizers (parity checks) and detect errors. Traditionally, because ancilla measurements themselves can be noisy, one would repeat this process $$d$$ times to be confident in the error syndrome.
In AFT, by doing only one round, the instantaneous state after that single round might not be a perfectly corrected codeword (some errors or syndrome mis-measurements could linger). However, the algorithm proceeds without pausing for additional checks – subsequent transversal operations continue, and further syndrome info is collected in later rounds as the circuit runs. Each logical operation thus incurs a fixed delay for one syndrome measurement, independent of $$d$$. This design dramatically raises the logical clock speed: for the surface code specifically, the authors report reducing syndrome rounds from $d$ to 1, directly cutting the space-time cost per logical gate.
Correlated Decoding and Exponential Error Suppression
How can skipping $$(d-1)$$ syndrome checks not compromise reliability? The answer lies in correlated decoding across the algorithm. Instead of decoding after each operation in isolation, AFT holds off on “final judgment” until a logical measurement is reached (e.g. the end of the algorithm or a major checkpoint). At that point, a joint classical decoder processes all the syndrome data from all rounds throughout the circuit to infer where errors likely occurred. This decoder takes into account correlations: an error that wasn’t fully corrected after one round will leave telltale patterns in later syndrome measurements. By correlating these patterns, the decoder can unravel errors that a single-round decode would miss. Essentially, AFT shifts some complexity to the decoder software, which does a global error correction pass covering the entire algorithm (or large chunks of it), rather than many separate local passes.
The result is that the final logical measurement outcomes are as reliable as in the traditional scheme with many rounds. The Nature paper proves that the deviation of the logical output distribution from the ideal (error-free) distribution can be made exponentially small in $$d$$, despite using only partial syndrome information at any given time.
In other words, even though the quantum state during the computation isn’t always forced back to a codeword after each gate, the output is virtually as good as if it had been. The logical error rate still drops exponentially with $$d$$. The Nature paper rigorously proves a suppression exponent proportional to d/4. However, the authors use the standard, more optimistic scaling of ~$${p_{\text{phys}}}^{(d+1)/2}$$ in their heuristic models for resource estimation, suggesting they anticipate the full error-correcting capability may be realized in practice.
The authors bolster this claim with circuit-level simulations, showing that their one-round-per-gate protocol achieves performance and error thresholds slightly reduced but still competitive with conventional multi-round methods. They even simulated full state distillation factories (used to produce magic states for universal computing) under AFT, finding little change in the error threshold compared to a standard surface-code memory.
This indicates that the AFT approach does not fundamentally weaken error suppression, it merely delays some error correction until later – an “algorithmic” form of fault tolerance that guarantees the final answer is correct with high probability.
Applicable Codes and Operations (CSS QLDPC Codes and Surface Code)
The AFT framework is quite general, but it does have some prerequisites. It applies to Calderbank-Shor-Steane (CSS) quantum LDPC codes – essentially any code where qubits participate in a limited number of checks and where the code structure allows transversal implementation of Clifford gates. The surface code (a high-density parity-check code on a 2D lattice) is a primary example and was a focus of the paper. Indeed, the authors show that even the surface code – often thought to require sequential syndrome cycles for fault tolerance – can run under AFT if we supply it with magic state inputs for non-Clifford operations.
In general, AFT handles universal quantum computing by assuming we can perform all Clifford gates transversally and teleport in magic states for the non-Clifford gates (like T gates). The surface code does not have a transversal T-gate (no code can have a fully transversal universal gate set, by the Eastin-Knill theorem), so this is handled by injecting a pre-prepared magic state when a T is needed, and then using a transversal Clifford (like a CNOT and measurement) to consume that state with feedforward logic.
Importantly, feedforward capability is assumed: the quantum circuit may include mid-circuit measurements (e.g. consuming a magic state) whose outcomes determine later operations. AFT accommodates this by performing partial decoding when a measurement occurs mid-computation, then using that result to adjust subsequent operations, all while keeping the one-round-per-step schedule. If a later global decode contradicts an earlier feedforward-based decision (i.e. it retroactively decides a measured qubit was in error), AFT has a method to reconcile this. The authors describe inserting Pauli corrections to “reinterpret” prior measurement results consistently.
In simpler terms, if the joint decoder later finds that a qubit’s measurement was wrong due to an undetected error, it can flip the interpretation of that result and adjust any dependent qubits so that the final outcomes remain logically correct. This ensures that feedforward operations (which are critical for universal computation with magic states) do not break the fault tolerance of the overall algorithm.
The need for transversal Clifford gates means the underlying code should support a set of gates that is powerful enough to execute the target algorithm’s Clifford part. Many CSS codes (including surface codes, color codes, and some LDPC codes) do allow transversal implementation of certain gates (e.g. the CNOT, or layer of Hadamards, etc.) The advantage of neutral atoms and some ion trap systems is that they can implement multi-qubit gates on distant qubits via reconfigurable interactions. This makes it feasible to perform a transversal gate even if the code’s qubits are not neighbors on a chip – one can physically rearrange or use long-range interactions (Rydberg links, ionic collective modes, etc.).
Thus, architecture matters: platforms with flexible connectivity can fully leverage transversal AFT without excessive routing overhead. In fact, the study specifically notes that neutral atoms and trapped ions have demonstrated native transversal gates and have relatively slow operation cycles, giving time to run more complex decoders concurrently. Superconducting qubit architectures, in contrast, might require more careful scheduling or additional swap networks to achieve the same effect, potentially reducing some of the space-time gains if not optimized.
Assumptions and Caveats
No approach is without trade-offs. The authors acknowledge several assumptions and open challenges:
- Efficient decoding algorithms: The fault-tolerance proof assumes using an optimal maximum-likelihood decoder (which in worst-case can be exponentially hard for general codes) and fast classical processing. The paper emphasizes that developing high-speed decoders is crucial going forward. In near-term demonstrations, the relatively long gate times of platforms like neutral atoms might allow the decoder to run in real-time, but for superconducting qubits (with sub-microsecond cycles) this could be a bottleneck.
- Magic state inputs: AFT assumes that magic states (non-Clifford ancillas) are provided with sufficiently low error rates (the paper calls them “low-noise magic state inputs”). In practice, magic states are distilled through intensive procedures that themselves require many qubits and cycles. The current AFT analysis largely treats magic states as an input resource and does not eliminate the overhead within the distillation process – though it hints that the same ideas might be applied to streamline that as well. In fact, the authors conjecture that certain magic state factory protocols could be run with fewer syndrome rounds using transversal gates. For now, one should note that AFT makes the use of magic states in circuits faster (only one check after injecting a state, rather than many), but the cost to produce those magic states remains, unless future work incorporates AFT into the distillation factories.
- Noise model: The fault-tolerance guarantees are proven under a standard local stochastic noise model. This essentially means errors occur randomly and independently with some probability, and larger correlated errors are exponentially suppressed. If the physical noise deviates strongly from this assumption (e.g. correlated errors affecting many qubits at once or adversarial burst errors), the performance of any QEC code, including under AFT, could be impacted. The transversal approach does ensure single physical errors don’t multiply, but it doesn’t magically prevent all forms of correlated noise. Likewise, AFT still assumes measurement errors occur and are of similar magnitude to gate errors; it simply deals with them differently.
- Transversal gate availability: While many codes have transversal implementations for Clifford gates, not every operation or code will fit the AFT framework. For instance, certain logical operations might not be transversal in a given code; one would then revert to other methods (or choose a code that supports a transversal version of that gate). The framework is most effective when a code and architecture support a rich set of transversal operations so that the majority of the circuit can be executed in this fashion. This may guide code design and hardware choices: codes that were previously overlooked due to lack of transversal gates for universality might be revisited if combined with magic-state injection for the non-transversal parts.
- Feedforward and adaptive control: Implementing AFT requires the ability to do quick feedforward – i.e. apply different gates conditioned on measurement outcomes during the computation. Many current quantum processors (including circuit-based superconducting and ion setups) do have this capability in their control systems, but it adds complexity. The classical control system must be tightly integrated to perform intermediate decodings and adjustments on the fly. Any latency in feedforward (especially for fast hardware) could effectively stall the processor. Thus, AFT puts emphasis on a robust classical co-processor that can handle decoding and decision-making at the pace of the quantum device.
Comparison with Prior Fault-Tolerance Approaches
The Algorithmic Fault Tolerance paradigm can be contrasted with existing fault-tolerance techniques:
- Versus “lattice surgery” and local gate gadgets: In conventional surface-code quantum computing, fault tolerance is often achieved through lattice surgery or braiding techniques. These involve multi-step sequences of measurements to enact logical operations like CNOTs or swaps between code patches. Each of those steps requires repeated syndrome cycles of order $$d$$ to be reliable, contributing to large space-time volume. By contrast, AFT avoids explicit surgery by using transversal gates (when possible) between code blocks directly, and by deferring error correction to a global decoder. This means an operation like a CNOT between two logical qubits can be done in one go (one round of checks afterward) instead of a lengthy surgical process. The trade-off is that AFT’s approach needs the ability to interact qubits from different patches transversally – feasible on a platform with flexible connectivity (e.g. movable atoms or ions) but not straightforward on a fixed grid. In essence, AFT favors a hardware-enabled transversal coupling over a software-based connecting of codes. Both approaches aim for the same fault-tolerant end result, but AFT can achieve it faster (constant time vs linear in $$d$$) if the hardware allows.
- Versus magic state distillation overhead: Magic state distillation is the standard method to generate the high-fidelity non-Clifford ancillas required for universal quantum computing. It typically incurs a huge overhead – factory circuits consuming thousands of qubits and many rounds of syndrome checks to output one magic state with error $$\ll 1/d$$. AFT can reduce the time overhead when using magic states (as discussed, injecting them with one round of checking). However, the distillation process itself in today’s schemes is like a sizable sub-computation that also needed multi-round verification. Some prior proposals (e.g. “constant-overhead” distillation or pieceable fault tolerance) tried to reduce that cost, but often at the expense of more qubits or complex code constructions. AFT’s authors suggest that their method could be extended to distillation too – for instance, by preparing the raw magic states with minimal checks and relying on correlated decoding to weed out errors in the output. If successful, that could eliminate another $$O(d)$$ overhead loop and significantly cut the overall resources for a full universal algorithm. In the meantime, the current achievement already integrates with magic state injection: once you have a magic state, you can teleport it into the computation with just one syndrome round post-teleport, trusting the decoder later to sort out any injection errors.
- Versus single-shot error correction: Single-shot QEC refers to codes or protocols that correct measurement errors in the same round as they are extracted – essentially achieving fault tolerance with one round of syndrome measurement. Some quantum LDPC codes (e.g. certain 3D codes or heavy‑hexagon varieties) have a single-shot property but often require complicated check operators or additional overhead in hardware. The AFT framework achieves a single-shot-like outcome (constant rounds) on standard codes that do not intrinsically have that property. It does so algorithmically rather than through code structure: by allowing a few extra errors to accumulate and using algorithm-level decoding to handle them. This is a big deal – it means we don’t necessarily need exotic new codes to avoid multiple rounds of checks; we can use well-studied codes like the surface code and still only do one round per step. The flip side is that AFT relies on more complex decoding and feedforward, as discussed. Single-shot codes might simplify decoding because they correct as they go, but they usually come at a cost of more complicated interactions or lower baseline threshold. In summary, AFT provides a general path to constant-time fault tolerance that is not limited to special single-shot codes, thus broadening the toolkit for architects. It shows that even without single-shot code properties, one can attain similar benefits by treating the whole algorithm coherently and exploiting transversality and correlation in decoding.
Why This Matters for Post-Quantum Risk Planners
For cybersecurity leaders and policymakers tracking quantum threats, this development is a (yet another) wake-up call. It directly addresses one of the main bottlenecks in building a CRQC – the huge time overhead of error correction – and demonstrates how to remove that bottleneck without new exotic hardware.
By doing so, it accelerates the timeline for fault-tolerant quantum computing, meaning that predictions may need another revision if such efficiency gains are realized in practice. In the words of the researchers, these results compel governments, HPC centers, and enterprises to “account for the accelerating timeline of fault-tolerant quantum computing in strategic planning.”
In practical terms, the window to implement post-quantum cryptography (PQC) might be tighter: a breakthrough that cuts overhead by 10× could bring a future quantum codebreaker from maybe a decade out to just a few years out once sufficient qubits are available. Risk planners should take note that neutral-atom platforms – which have long been seen as scalable but slow – might leap ahead with this approach, delivering large-scale cryptanalysis capabilities sooner than expected.
The race between quantum code-makers and code-breakers just got a lot faster.
Quantum Upside & Quantum Risk - Handled
My company - Applied Quantum - helps governments, enterprises, and investors prepare for both the upside and the risk of quantum technologies. We deliver concise board and investor briefings; demystify quantum computing, sensing, and communications; craft national and corporate strategies to capture advantage; and turn plans into delivery. We help you mitigate the cquantum risk by executing crypto‑inventory, crypto‑agility implementation, PQC migration, and broader defenses against the quantum threat. We run vendor due diligence, proof‑of‑value pilots, standards and policy alignment, workforce training, and procurement support, then oversee implementation across your organization. Contact me if you want help.



