The Controlled-NOT (CNOT) Gate in Quantum Computing

Introduction

Quantum computing is poised to revolutionize the field of cybersecurity – both by breaking some of today’s encryption and by offering new, physics-based security protocols. Unlike classical computers, which use bits that are either 0 or 1, quantum computers use quantum bits (qubits) that leverage phenomena like superposition and entanglement to perform computations beyond classical capabilities. This power comes with a double-edged sword for security: on one hand, a sufficiently large quantum computer could crack widely used cryptographic algorithms (for example, Shor’s algorithm can factor large numbers, threatening RSA encryption), and on the other hand, quantum mechanics enables new secure communication methods like quantum key distribution (QKD). Governments and industry are taking note – the U.S. Department of Homeland Security has even identified the transition to post-quantum encryption as a priority to ensure cyber resilience.

With quantum computing advancing rapidly, it’s crucial for cybersecurity professionals to grasp its fundamentals. In particular, understanding the Controlled-NOT (CNOT) gate – one of the most important two-qubit logic gates – is essential. The CNOT gate is to quantum circuits what the XOR gate is to classical circuits: a basic building block for complex operations. By learning how the CNOT gate works and why it matters, cybersecurity experts can better appreciate how quantum computers process information, how they might break cryptography, and how they enable new secure protocols. This article provides an accessible yet rigorous overview of the CNOT gate, tailored for tech-savvy professionals in security.

Foundational Quantum Concepts

Before diving into the CNOT gate, let’s briefly review a few quantum computing basics: qubits, superposition, and entanglement. A qubit (quantum bit) is the quantum analogue of a classical bit. While a classical bit is either 0 or 1, a qubit can exist in a superposition of 0 and 1 – essentially being in both states at the same time until measured. One intuitive analogy is a coin flip: a classical bit is like a coin lying heads or tails up, whereas a qubit is like a coin spinning in mid-air, temporarily representing both heads and tails at once. In mathematical terms, if we denote the state “0” as |0⟩ and “1” as |1⟩, a qubit’s state can be a combination (linear combination) of the two, e.g.  |ψ⟩ = α|0⟩ + β|1⟩, where α and β are complex probability amplitudes. Only when you measure the qubit does it “collapse” to either |0⟩ or |1⟩ with probabilities |α|² and |β|² respectively. This superposition property is what gives quantum computers their parallelism – a collection of qubits can represent many values simultaneously, enabling certain computations (like brute-forcing keys or factoring) to be done much faster than on classical machines.

Entanglement is a second fundamental concept critical to quantum computing (and quantum cryptography). Entanglement is a phenomenon where two or more qubits become linked such that the state of one qubit is dependent on the state of the other, no matter how far apart they are. In an entangled pair, neither qubit has a definite value by itself; they only have a well-defined state as a combined system. As a result, measuring one instantly influences the state of the other – a kind of correlation that has no classical equivalent. For example, imagine two qubits that are entangled in a state where they are correlated to always have opposite values. If one yields 0 upon measurement, the other will immediately yield 1, even if it’s on the other side of the world. Einstein famously dubbed this “spooky action at a distance.” In more technical terms, entangled qubits share a single joint quantum state that cannot be factored into independent states for each qubit. This means their outcomes are perfectly correlated in a way that cannot be explained by any pre-existing agreement (a fact proven by Bell’s Theorem). Entanglement is not just a curiosity – it’s a resource. It enables quantum computers to perform operations that classical computers cannot easily simulate, and it’s the basis for quantum cryptographic protocols where any eavesdropping can be detected (since an outsider’s interference disturbs the entangled state). In fact, entanglement is “a necessary ingredient of any quantum computation that cannot be done efficiently on a classical computer.” In other words, without entanglement, a quantum computer would lose its advantage. As we’ll see, the CNOT gate is one of the primary ways to create entanglement between qubits.

What is the CNOT Gate?

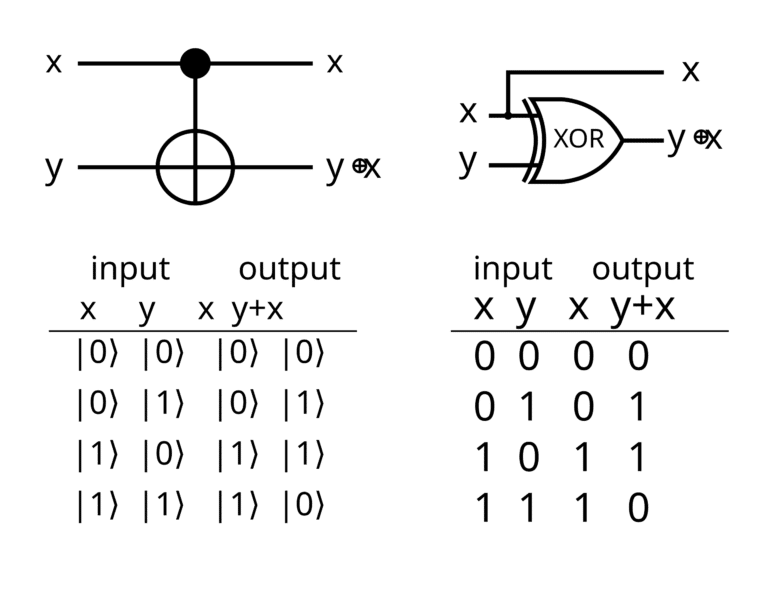
The Controlled-NOT (CNOT) gate is a two-qubit quantum logic gate, sometimes also called the controlled-X gate or Feynman gate. It operates on a pair of qubits: one designated as the control qubit and the other as the target qubit. The CNOT performs a simple but powerful operation: it flips the state of the target qubit (i.e., applies a quantum NOT operation, which is the Pauli-X gate) if and only if the control qubit is in the state |1⟩. If the control qubit is |0⟩, the target is left unchanged. In essence, the control qubit “controls” whether a NOT (bit-flip) is applied to the target.

This behavior is directly analogous to a classical XOR operation. If we consider the basis states |0⟩ and |1⟩ as binary 0 and 1, then CNOT transforms an input pair (control, target) as follows:

• If the control is 0: (0, b) → (0, b). (Target bit b stays the same.)
• If the control is 1: (1, b) → (1, not b). (Target bit b is flipped from 0 to 1 or 1 to 0.)

In other words, the target output bit is the XOR of the original control and target bits, while the control output remains the same. This is why the classical analogue of CNOT is a reversible XOR gate. (If the control is fixed to 1, CNOT simply acts as a NOT on the target.) Importantly, CNOT is reversible – given the output, you can unambiguously recover the inputs, which is a requirement for any quantum gate (since quantum evolutions are reversible/unitary).

In quantum terms, the CNOT gate’s action can be described in terms of basis states |00⟩, |01⟩, |10⟩, |11⟩ (where the first bit is the control and second is the target). It maps these four two-qubit basis states as:

• |00⟩ → |00⟩
• |01⟩ → |01⟩
• |10⟩ → |11⟩  (control 1 causes target 0 to flip to 1)
• |11⟩ → |10⟩  (control 1 causes target 1 to flip to 0)

We can represent this operation with a 4×4 matrix (in the ordered basis |00⟩, |01⟩, |10⟩, |11⟩). The CNOT gate’s matrix is:

This matrix shows that CNOT leaves |00⟩ and |01⟩ unchanged (the 1’s in the first two diagonal entries), while it swaps |10⟩ and |11⟩ (the off-diagonal 1’s in the last 2×2 block). If you apply this matrix to a two-qubit state vector, it will flip the amplitudes of |10⟩ and |11⟩ components, corresponding to flipping the target qubit when the control is 1.

Another way to visualize the CNOT is by its quantum circuit symbol, which is commonly used in quantum circuit diagrams. The control qubit’s wire (horizontal line) gets a solid black dot (●), and the target qubit’s wire gets a circled plus sign (⊕) indicating the NOT operation. A vertical line connects the ● (control) to the ⊕ (target). This notation succinctly shows that the target undergoes an X (NOT) conditioned on the control being 1. So whenever you see ●──⊕ in a quantum circuit, that’s a CNOT gate between those two qubits.

The CNOT gate has a few key properties worth noting: it is a unitary operation (like all quantum gates), meaning it preserves the total probability and has a well-defined inverse (in fact, CNOT is its own inverse – performing it twice in a row returns the qubits to their original states). It is also a two-qubit entangling gate, which means that by acting on certain input states, it can produce entanglement between the control and target qubits. This last point is especially important, as we discuss next.

Why is the CNOT Gate Fundamental?

The CNOT gate is often described as one of the workhorses of quantum computing. There are a few big reasons for this:

1. CNOT generates entanglement – the magic ingredient in quantum computing. As discussed, entanglement is essential for quantum computational advantage and quantum cryptography. The CNOT gate is one of the simplest ways to create entangled states. For example, consider two qubits initially in the state |00⟩ (both qubits are 0). If we apply a Hadamard (H) gate to the first qubit (the control), it goes into a superposition: H|0⟩ = (|0⟩ + |1⟩)/√2, so our two-qubit state becomes (|00⟩ + |10⟩)/√2 (the control is in a superposition of 0 and 1, and the target is still 0). Now apply a CNOT with the first qubit as control and second as target. The CNOT will flip the target qubit only for the |10⟩ component of the superposition. The resulting state is (|00⟩ + |11⟩)/√2, which is one of the famous Bell states (specifically, the state often denoted Φ^+). This state is maximally entangled – if measured, both qubits always yield the same result, 00 or 11, with equal probability. We have thus engineered entanglement using a CNOT gate. In fact, the CNOT is so good at entangling and disentangling qubits that it can be used to create all four Bell states (by varying inputs), and to convert entangled states back into separable ones. In general, whenever you hear about two qubits being entangled in a quantum algorithm or protocol, there’s a good chance a CNOT (or similar two-qubit gate) is involved in the process. Without an entangling gate like CNOT, qubits would remain independent, and a quantum computer would effectively act like a probabilistic classical computer rather than exploiting true quantum effects. As a reminder of its importance: “Any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and single qubit rotations.” In other words, CNOT together with one-qubit gates forms a universal set – capable of constructing any arbitrary multi-qubit operation.

2. CNOT enables universal quantum logic. In classical computing, we have universal gates (like NAND) that can be combined to implement any logical function. In quantum computing, universality works a bit differently, but the CNOT plays a key role analogous to that of NAND in classical logic. It turns out that any multi-qubit quantum operation can be decomposed into a network of CNOT gates plus single-qubit gates (such as rotations, Hadamards, and phase gates). For example, a CNOT can entangle qubits, while single-qubit gates can create superpositions and adjust phases. This is sufficient to build up any quantum computation. The CNOT by itself isn’t universal (just as XOR alone isn’t universal classically – you can’t get an AND from just XORs without some constant bits), but {CNOT + all single-qubit gates} is universal for quantum computing. In practice, many quantum algorithms (like Grover’s or Shor’s) when compiled to circuits will have dozens or millions of CNOT gates creating entanglement between qubits to carry out the logic. In fact, entangling gates like CNOT are typically the most “expensive” operations in quantum hardware, and a large part of quantum computer engineering is making CNOT gates as high-fidelity as possible. Without CNOT (or another entangling two-qubit interaction), qubits cannot be entangled and a quantum computer would just be a bunch of independent 1-qubit systems. This is why CNOT is fundamental: it’s the gate that stitches the qubits together into a single computational fabric. The importance of entanglement generated by CNOT can’t be overstated: entanglement is required for quantum computations that outperform classical ones. No entanglement means no exponential advantage. Thus, CNOT is indispensable for enabling the “quantum” in quantum computing.

3. CNOT is involved in nearly every quantum algorithm and protocol. Whether it’s for entangling qubits as part of a quantum Fourier transform, performing a conditional operation in an algorithm, or encoding data in an error-correcting code, the CNOT gate (or its close cousins) show up everywhere. Its ability to condition one qubit’s operation on the state of another is the basis of “if-then” logic in quantum circuits – much like an if-statement in software. For instance, in phase estimation (a subroutine of Shor’s algorithm), CNOTs are used to encode the phases; in the quantum teleportation protocol, CNOT is used to entangle the sender’s qubit with an auxiliary qubit; and in creating GHZ states (to be discussed later), CNOTs are applied in sequence to spread entanglement across multiple qubits. Whenever you read about a quantum computer entangling qubits or performing a conditional operation, think of the CNOT gate.

In summary, the CNOT gate’s ability to flip a target qubit based on a control qubit seems simple, but this conditional logic is the backbone of quantum algorithms. It enables qubit interactions, entanglement generation, and ultimately the complex interference patterns that give quantum computing its power.

How Other Logical Gates Can Be Constructed with CNOT

The CNOT gate is not only useful on its own – it is a key component in building other, more complex quantum logic gates. In fact, a variety of multi-qubit gates and operations can be constructed using CNOT gates combined with single-qubit gates. Cybersecurity professionals don’t need to design circuits themselves, but understanding this composability is helpful to see why CNOT is considered so fundamental. Here are a few notable examples of logic constructions involving CNOT:

Reversible XOR (Controlled-NOT itself): As mentioned, the CNOT gate is essentially the quantum (and reversible) version of an XOR gate. If we label the input bits as A (control) and B (target), after CNOT the outputs are A (unchanged) and A⊕B (A XOR B) – with the crucial difference that in quantum, A can be a superposition and B⊕A will accordingly be in a superposition of results. This reversible XOR (sometimes called the Feynman gate in reversible computing) is often used within larger circuits as a building block for addition or parity checks. Because CNOT doesn’t destroy the original control bit (it “fans out” the information via entanglement rather than copying it, in accordance with the no-cloning theorem), it’s extremely useful in quantum logic designs.

NOT and Conditional NOT: A single CNOT can act as a controlled-NOT. If the control qubit is set to |1⟩ (and not allowed to vary), then the CNOT just flips the target – behaving exactly like a regular NOT gate on the target bit. Conversely, if the target is initialized to |0⟩, the CNOT will copy the control qubit’s state onto the target (because the target flips to match the control if the control is 1, and stays 0 if the control is 0). In this way, CNOT can be used to clone classical bits (though it cannot clone arbitrary quantum states). This is useful for distributing classical information in reversible computing or for creating entangled pairs when combined with superposition inputs.

SWAP Gate: A SWAP gate exchanges the states of two qubits. Surprisingly, you can implement a SWAP using three CNOT gates in sequence. Suppose we have two qubits Q1 and Q2 that we want to swap. The sequence is: CNOT(Q1 → Q2), then CNOT(Q2 → Q1), then CNOT(Q1 → Q2) again. After these three operations, the net effect is that whatever state Q1 started in ends up in Q2, and vice versa. (All three CNOTs are needed; performing only two would entangle the qubits instead of fully swapping them.) The SWAP operation is useful in quantum circuits for routing qubits (especially in hardware with limited connectivity). That it can be decomposed into CNOTs demonstrates how CNOT serves as a basic ingredient for even symmetric operations like swapping two values.

Toffoli Gate (Controlled-Controlled-NOT): The Toffoli gate is a three-bit gate (two controls and one target) that flips the target if and only if both control qubits are 1. It’s essentially a controlled version of CNOT itself (a 2-control, 1-target gate). The Toffoli is important because it’s universal for classical reversible computation – you can build any reversible Boolean circuit using Toffoli gates. In the quantum realm, a Toffoli gate can be constructed using multiple CNOT gates plus some single-qubit rotations. One known decomposition uses at least 6 CNOT gates along with some Hadamard and T (π/8 phase) gates. While we won’t delve into the exact sequence, the key point is that CNOT is a crucial component of Toffoli. In fact, it has been proven that you need at least five two-qubit gates to build a Toffoli, and typical constructions use six or more – many of which are CNOTs. Whenever you hear about a multi-controlled operation, e.g. a gate that does something if qubit A and qubit B are 1, behind the scenes it’s usually broken down into CNOTs and single-qubit gates. The ability to combine CNOTs to create a Toffoli means we can also build any classical logic function (like AND, OR, XOR combinations) reversibly on a quantum computer – an important feature for algorithms that include classical subroutines or for error correction circuits.

Controlled-Z and other Controlled Gates: A controlled-Z (CZ) gate flips the phase of the target qubit (applies a Pauli-Z) if the control is 1. It’s another common two-qubit gate. You can turn a CNOT into a CZ (or vice versa) using single-qubit basis changes. For example, if you surround the target of a CNOT with Hadamard gates (H before and H after), the X flip is converted into a Z flip, effectively yielding a CZ gate. This shows that CNOT is inter-convertible with other controlled two-qubit operations given appropriate 1-qubit rotations. Similarly, a CNOT with the control and target swapped (which is not the same as a regular CNOT, since CNOT is not symmetric in its inputs) can be achieved by conjugating with Hadamards on both qubits. The general idea is that CNOT + single-qubit gates = any controlled unitary. This flexibility makes CNOT a universal two-qubit entangler.

In summary, many complex gates can be reduced to combinations of CNOTs. From a cybersecurity perspective, this means that any quantum circuit you hear about – whether it’s implementing a cryptographic algorithm, an error-correcting code, or a quantum communication protocol – likely has CNOT gates under the hood. CNOT is the “glue” that lets qubits interact and therefore is present whenever multi-qubit logic or entanglement is needed.

Role in Quantum Cryptography & Error Correction

Finally, let’s look at two critical domains for cybersecurity where the CNOT gate plays a starring role: quantum cryptography (in particular QKD and related protocols) and quantum error correction, which is vital for building stable quantum computers that can run algorithms to break cryptography.

CNOT in Quantum Cryptography (QKD and GHZ States)

Quantum cryptography leverages quantum mechanics to achieve security guarantees that are impossible with classical physics. The most well-known example is Quantum Key Distribution (QKD) – a method for two parties to generate a shared secret key such that any eavesdropping attempt is detectable. There are different types of QKD protocols, but one class uses entangled photon pairs (for example, the Ekert E91 protocol). How do we create entangled pairs for such a protocol? Conceptually, we use the same method described earlier: take two qubits, put one in a superposition, and apply a CNOT to entangle them into a Bell state. In practice, hardware might use a spontaneous photon pair source, but the effect is equivalent to having applied a CNOT gate to produce an entangled pair of qubits shared between Alice and Bob. These entangled pairs have the property that measurements by Alice and Bob are correlated. If an eavesdropper (Eve) tries to intercept or measure these entangled qubits in transit, she will inevitably disturb their state and introduce anomalies that Alice and Bob can detect when they compare some of their measurement results. This is the basis of security in entanglement-based QKD: any interception breaks the entanglement, alerting the legitimate parties. In fact, the entanglement principle applied to QKD can be summarized: the key for encrypted data decryption is shared through entangled particles, and any attempt to intercept the particles triggers a change in their state, alerting the parties to a breach. CNOT is instrumental here because it’s a primary tool to generate those entangled pairs (e.g., by entangling two photons or two qubits before sending one to Bob). Without an operation like CNOT, we wouldn’t have a straightforward way to produce the entangled keys that give QKD its eavesdropper-detection ability.

Beyond two-party QKD, entangling gates enable more complex cryptographic schemes. GHZ states (Greenberger–Horne–Zeilinger states) are entangled states of three (or more) qubits, for example the three-qubit state (|000⟩ + |111⟩)/√2. A GHZ state can be created by extending the Bell state: for instance, if you already have two qubits entangled (|00⟩ + |11⟩)/√2, applying a CNOT from one of those qubits to a third qubit (initially |0⟩) will bring the third qubit into the entangled state as well, yielding (|000⟩ + |111⟩)/√2. GHZ states have intriguing applications in quantum cryptography and communication. One example is quantum secret sharing, where a secret key is distributed among multiple parties such that only by combining their information (each has one qubit of a GHZ state, for instance) can they reconstruct the key – if one party is compromised or an outsider intercepts one qubit, the remaining information is insufficient to get the key, and the disturbance can be detected. Another example is in quantum network protocols or digital signatures: there are proposals for quantum digital signature schemes that use GHZ entangled particles to ensure security and authenticity. The security of these schemes often rests on the property that GHZ states exhibit strong correlations and obey the monogamy of entanglement (meaning if three qubits are maximally entangled in a GHZ state, an outsider cannot entangle with them without breaking the original entanglement). Achieving these multi-qubit entangled states in practice invariably relies on sequences of two-qubit gates like CNOT. Thus, CNOT is enabling not just pairwise security protocols but also multi-party cryptographic protocols. As quantum networks grow, we may see entanglement-based schemes (like conference key agreement or distributed quantum encryption) that use clusters of entangled qubits – all of which would be prepared using fundamental gates like CNOT.

In summary, for quantum cryptography: whenever we create entangled bits for secure key exchange or other protocols, the CNOT gate is at play. Its ability to entangle is the bedrock of the security in quantum security systems. For cybersecurity experts, this is a fascinating flip side: the same mechanism (entanglement via CNOT) that can threaten classical encryption by powering a quantum computer is also what can protect communications in the quantum realm. Understanding CNOT gives insight into how entangled keys are made and why they’re secure.

CNOT in Quantum Error Correction

On the other end of the spectrum, CNOT is vital for quantum error correction (QEC). Quantum error correction is what will allow quantum computers to scale to the sizes needed to run cryptography-breaking algorithms reliably. It’s analogous to error-correcting codes in classical communications, but complicated by the fact that directly measuring qubits to check for errors destroys their superposition state. QEC codes get around this by encoding a logical qubit into multiple physical qubits in an entangled state such that if one qubit undergoes an error (like a flip or a phase change), the error can be detected and corrected without revealing the logical information.

How do we create these encoded, entangled states? Enter the CNOT gate. For a simple example, consider the three-qubit bit-flip code (which protects against one bit-flip error, akin to a classical repetition code of “0” to “000” or “1” to “111”). To encode a single qubit |ψ⟩ = α|0⟩ + β|1⟩ into a three-qubit state, we start with the original qubit and two additional qubits initialized to |0⟩ (ancilla qubits). Then we apply CNOT gates from the original qubit to each of the two ancillas. If the original qubit was |0⟩, nothing happens and we end up with |000⟩; if the original was |1⟩, the CNOTs flip both ancillas to 1, yielding |111⟩. Under superposition, α|0⟩ + β|1⟩ becomes α|000⟩ + β|111⟩ – an entangled 3-qubit state that encodes the information. This mapping (|0⟩→|000⟩, |1⟩→|111⟩) is achieved using two CNOT gates to entangle the original qubit with the ancillaries. Now, if any one of these three qubits accidentally flips (say due to noise), the error can be detected by checking the parity of the qubits (using additional CNOTs and measurements) without measuring the qubits directly. The CNOT gate is used in those parity checks as well – essentially performing XORs between qubits onto a measurement ancilla to see if they differ. A similar procedure using controlled-phase (which can also be done via CNOT in a different basis) can protect against phase flips. Peter Shor’s famous 9-qubit code combines two levels of encoding (bit-flip and phase-flip) and heavily employs CNOT gates and Hadamards to achieve an error-resilient encoding. In Shor’s code, one logical qubit is encoded into 9 physical qubits using a sequence of CNOTs that first create three sets of |000⟩/|111⟩ triplet states and then entangle those triplets in the Hadamard-transformed basis. The end result is a highly entangled 9-qubit state that can correct any single-qubit error. Every step of that encoding involves CNOT gates to spread out the quantum information and entangle qubits so that errors can be detected as syndromes (patterns of parity flips) on ancillary measurements.

Furthermore, in the operation of error correction, after encoding, one periodically checks for errors (syndrome measurement). How do you check if two qubits have the same value (which could indicate an error if they differ)? You use a CNOT: you CNOT both data qubits onto an ancilla (or two ancillas) and measure the ancilla(s). This tells you the parity (XOR) of the qubits without directly measuring them. This is essentially the quantum equivalent of a checksum and is a core part of stabilizer codes like the Steane code or surface codes. Again, CNOT is performing the role of parity parity calculator via entanglement – it correlates the ancilla with the parity of the data qubits. If an odd parity (meaning an error likely occurred on one qubit) is detected, further CNOTs can be used to correct the error by flipping the affected qubit.

From a cybersecurity viewpoint, quantum error correction is what will make large-scale quantum computers viable – and thus what will ultimately determine if and when quantum computers can break current cryptography. It’s notable that the very same gate (CNOT) that we fear being used millions of times to run Shor’s algorithm is also the gate that engineers are using to implement error correction to enable those algorithms to run. Error correction codes are essentially algorithms for reliability, and they run on quantum computers as sets of quantum gates (the term “quantum error-correcting code” might sound abstract, but in practice it’s a specific circuit of CNOTs and other gates that continually checks and fixes errors). Every time an error is corrected, entanglement and CNOTs are involved in detecting and propagating the information about the error without destroying the quantum data.

To recap, CNOT’s role in QEC is to facilitate encoding (distributing quantum information across multiple qubits by entangling them) and syndrome measurement (retrieving error information via parity checks). Without CNOT, we couldn’t create the redundancy or perform the checks needed for error correction. Thus, CNOT is a linchpin in the effort to build reliable, large-scale quantum computers – the very machines that pose a risk to our cryptographic infrastructure.

Conclusion

Quantum computing introduces new paradigms that are both exciting and challenging for cybersecurity. The Controlled-NOT (CNOT) gate, while just one component of the quantum toolbox, encapsulates many of those paradigms: superposition (through its action on quantum superposed inputs), entanglement (as a direct product of its operation), and reversibility. We’ve seen that the CNOT gate is essential for implementing quantum logic: it’s the mechanism by which qubits talk to each other and by which quantum algorithms gain their non-classical power. For cybersecurity professionals, a solid understanding of the CNOT gate and its implications provides a foundation for grasping how quantum computers operate and how they impact security:

Quantum algorithms and cryptanalysis: CNOT gates (in tandem with one-qubit gates) build the circuits for algorithms like Shor’s factoring or Grover’s search. Knowing that CNOTs create entanglement helps one appreciate why quantum algorithms can process certain problems (like factoring large integers, which underpins RSA) so much faster – because they leverage entangled qubits to examine multiple possibilities in parallel and then interfere to get the answer. When you hear about a quantum circuit with a hundred qubits factoring a number, imagine a complex network of CNOT gates entangling those qubits. Understanding CNOT is understanding the “XOR logic” and entangling fabric that threatens classical encryption.

Quantum cryptography: Conversely, protocols like QKD use entanglement (often generated by CNOT operations at a conceptual level) to provide fundamentally secure key exchange. As quantum networking grows, cybersecurity experts may be tasked with implementing or evaluating QKD systems or other entangled-state cryptosystems. Recognizing that a CNOT gate could be creating the entanglement used in, say, an entangled-photon QKD system helps demystify how measurement of one particle affects the other and reveals eavesdropping. In multi-party settings, understanding gates like CNOT gives insight into how multi-qubit entangled states (GHZ, etc.) are prepared and why they are useful for things like secret sharing or distributed consensus with security.

Quantum error correction and defense: The timeline for quantum computers breaking encryption is heavily dependent on error correction. Each logical qubit in a fault-tolerant quantum computer might require hundreds or thousands of physical qubits entangled via CNOT gates in an error-correcting code. For those in cybersecurity, keeping an eye on progress in quantum error correction (and thus the fidelity and scalability of CNOT gates) can inform estimates of when quantum attacks might become feasible. Moreover, for those who venture into quantum-resistant security, familiarity with how quantum computers are built (with gates like CNOT and others) can help in understanding the limitations and practical challenges quantum computers face.

In short, the CNOT gate is a gateway (pun intended) to understanding quantum computing’s impact on security. It’s remarkable that a single gate – flipping a qubit conditional on another – enables such a rich tapestry of phenomena: entangled states that defy classical explanation, computations that solve problems exponentially faster, and protocols that achieve unbreakable encryption keys.