Qubits: A Brief Introduction for Cybersecurity Professionals
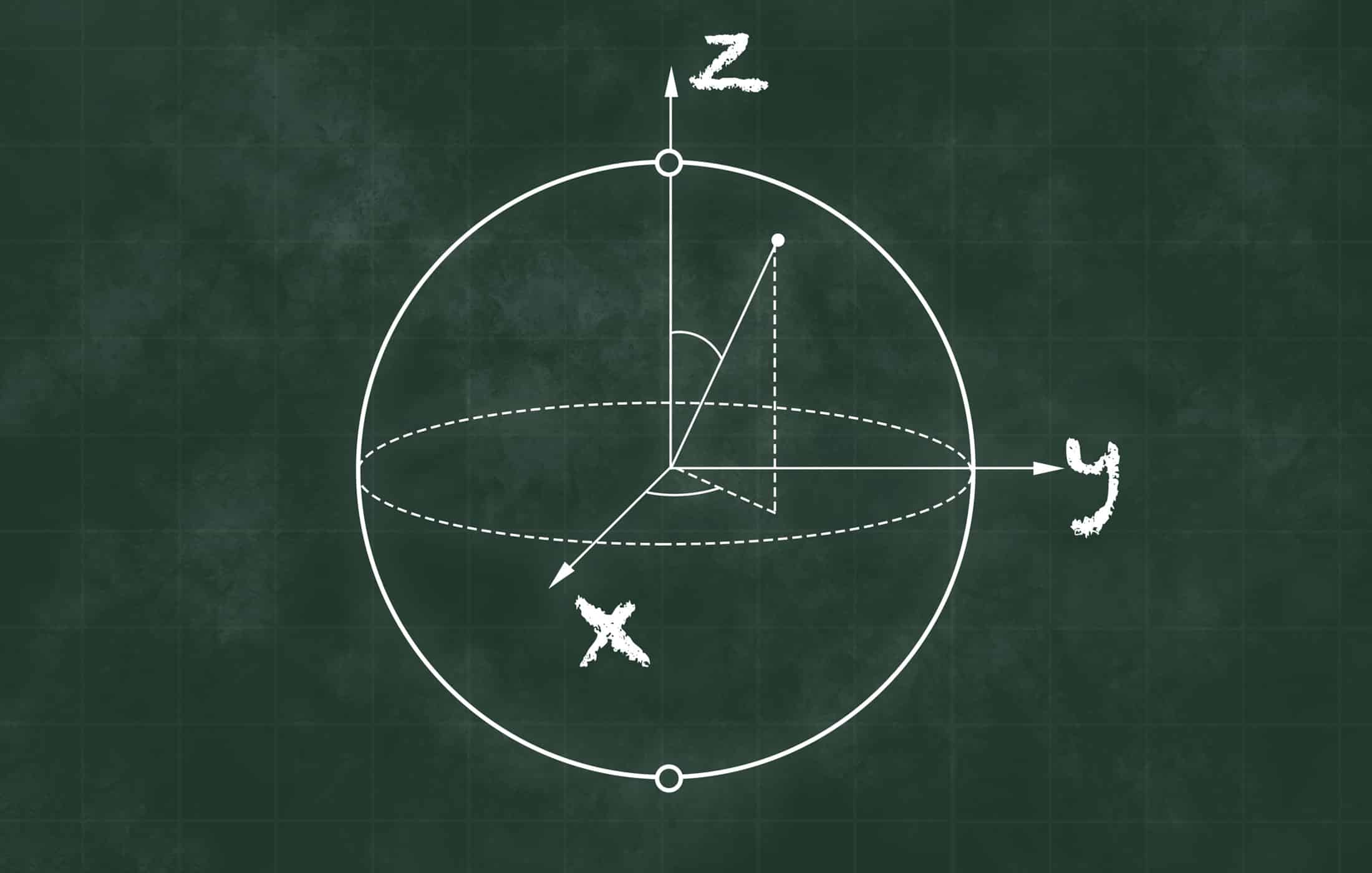
Table of Contents
Introduction
Quantum computing is an emerging field that promises to solve certain problems far faster than classical computers. Its fundamental unit of information is the qubit (quantum bit). For cybersecurity professionals, understanding qubits and their properties is key to grasping how quantum technologies might impact encryption, secure communications, and cryptography. This article introduces what qubits are, how they are described mathematically, key quantum operations, and why they matter in cybersecurity.
What Is a Qubit (and How Is It Different from a Bit)?
A qubit is the quantum analog of a classical bit – it’s the basic unit of quantum information. However, unlike a classical bit that can only be 0 or 1 at any given time, a qubit can exist in a combination of both 0 and 1 states simultaneously. This property is called superposition. In practical terms, a classical binary bit has to be in one of two possible states (0 or 1), whereas a qubit can represent 0, 1, or any proportion of 0 and 1 at the same time, with certain probabilities for each. This means a qubit holds more information than a bit because it can explore many states at once until it’s measured. In essence, quantum mechanics allows a qubit to be in multiple states simultaneously, which is a fundamental departure from classical computing behavior.
Mathematical Representation of a Qubit
State Superposition Notation
Quantum states are often described using Dirac bra-ket notation. A single qubit’s state is written as:
$$∣ψ⟩=α ∣0⟩+β ∣1⟩,|\psi\rangle = \alpha\,|0\rangle + \beta\,|1\rangle,∣ψ⟩=α∣0⟩+β∣1⟩$$,
where $$∣0⟩|0\rangle∣0⟩$$ and $$∣1⟩|1\rangle∣1⟩$$ are the two basis states (read “ket 0” and “ket 1”), and α and β are complex numbers called probability amplitudes. These amplitudes determine the probability of the qubit being found in each basis state upon measurement. The key constraint is that $$∣α∣2+∣β∣2=1|\alpha|^2 + |\beta|^2 = 1∣α∣2+∣β∣2=1$$, ensuring the probabilities sum to 100%. For example, if $$∣α∣2=0.7|\alpha|^2 = 0.7∣α∣2=0.7$$ and $$∣β∣2=0.3|\beta|^2 = 0.3∣β∣2=0.3$$, the qubit has a 70% chance of being observed as 0 and 30% as 1 when measured. Until measurement, however, the qubit is in a superposition of both 0 and 1 states simultaneously as described by the combination $$α∣0⟩+β∣1⟩ \alpha|0\rangle + \beta|1\rangleα∣0⟩+β∣1⟩$$.
Bloch Sphere Representation
Another way to understand a qubit state is via the Bloch sphere, a visual tool to represent the state of a two-level quantum system. The Bloch sphere is an imaginary unit sphere where any point on its surface corresponds to a unique pure qubit state. Think of the north pole of the sphere as the state $$∣0⟩|0\rangle∣0⟩$$ and the south pole as $$∣1⟩|1\rangle∣1⟩$$. Any other point on the sphere’s surface represents a superposition of $$∣0⟩|0\rangle∣0⟩$$ and $$∣1⟩|1\rangle∣1⟩$$. For instance, points along the equator might correspond to states like an equal superposition (where $$∣α∣2=∣β∣2=0.5|\alpha|^2 = |\beta|^2 = 0.5∣α∣2=∣β∣2=0.5$$). The Bloch sphere helps visualize a qubit’s state and phase: moving around the sphere changes the qubit’s state continuously. This representation is widely used because it intuitively shows operations on qubits as rotations of the state vector on the sphere. For a cybersecurity professional, it’s not critical to master the mathematics of the Bloch sphere, but it’s useful to know that single-qubit states can be visualized geometrically on this sphere, with superposition states occupying all the points between the classic 0 and 1 poles.
Key Quantum Concepts: Superposition, Entanglement, and Measurement
Qubits exhibit several non-intuitive quantum phenomena that have no equivalent in classical bits. The most important concepts are superposition, entanglement, and measurement (collapse):
- Superposition: As noted, a qubit can exist in a superposition of states, meaning it holds a combination of 0 and 1 until observed. This is not an operation per se, but a core property. In practice, quantum operations (gates) like the Hadamard gate can put a qubit into a superposition of $$∣0⟩|0\rangle∣0⟩$$ and $$∣1⟩|1\rangle∣1⟩$$. Superposition enables quantum computers to process many possibilities at once. For example, two qubits in superposition can collectively represent four possible values simultaneously (00, 01, 10, 11) due to their combined state space. This parallelism is a source of quantum computing’s potential power.
- Entanglement: Entanglement is a phenomenon that occurs when you have two or more qubits such that their states become linked together. An entangled pair of qubits behaves as one system: measuring one instantly affects the state of the other, no matter how far apart they are. In an entangled state, the outcome of one qubit is correlated with the outcome of the other. For instance, two qubits might be prepared in an entangled state where they are always observed to be opposite (if one is 0, the other is 1, and vice versa). If these qubits are separated (even by large distances) and one is measured, the other’s state is immediately determined. Entangled qubits thus share a single unified state – measuring one yields information about the other without any further communication. Entanglement is a resource that quantum algorithms and quantum cryptographic protocols (like certain QKD schemes) exploit, and it has no parallel in classical computing.
- Measurement and Collapse: Measuring a qubit forces it to “decide” on a definite state (much like checking reveals a coin toss outcome). When you measure a qubit’s value, the superposition collapses to a classical result of either 0 or 1. The probabilities of getting 0 or 1 are given by the amplitudes $$∣α∣2|\alpha|^2∣α∣2$$ and $$∣β∣2|\beta|^2∣β∣2$$ from the qubit’s state. For example, measuring the state $$α∣0⟩+β∣1⟩\alpha|0\rangle + \beta|1\rangleα∣0⟩+β∣1⟩$$ will yield $$∣0⟩|0\rangle∣0⟩$$ with probability $$∣α∣2|\alpha|^2∣α∣2$$ and $$∣1⟩|1\rangle∣1⟩$$ with probability $$∣β∣2|\beta|^2∣β∣2$$. After measurement, the qubit will remain in whichever state it collapsed to (the superposition is lost). An important aspect of quantum measurement is that it irreversibly disturbs the system – you generally cannot measure a qubit without altering its state. This has direct implications for security (as we’ll see with QKD): any observation by an eavesdropper changes the qubit’s state, making their presence detectable.
Relevance to Cybersecurity: Quantum Crypto and Post-Quantum Preparedness
Quantum computing and qubits aren’t just abstract physics – they carry real significance for cybersecurity. Two areas of particular importance are quantum cryptography (using qubits for new secure communication methods) and post-quantum cryptography (adapting our current security to withstand quantum attacks):
Quantum Key Distribution (QKD)
QKD is the best-known application of qubits in cybersecurity. It leverages quantum properties to enable two parties to share encryption keys with provable security. In QKD, information (key bits) is encoded in qubits (often using photons) and sent across a channel. The power of QKD lies in the fact that any eavesdropping attempt will disturb the qubit states. Because of quantum physics (e.g. the no-cloning theorem and measurement disturbance), an eavesdropper cannot intercept qubits without introducing anomalies. In other words, if an attacker tries to spy on the key exchange, they will inevitably alter the qubits’ state and introduce errors that the legitimate participants can detect. This alert allows the communicating parties to discard the compromised key and try again, ensuring that only the intended recipients share the final key. QKD, such as the BB84 protocol, is thus an eavesdropper-detecting key exchange mechanism. In theory, as long as the laws of physics hold, QKD can provide unbreakable encryption keys. However, QKD does require specialized hardware (like photons traveling in fiber) and is currently practical only for certain high-security, short-distance links. Still, it highlights how qubits enable new cryptographic techniques fundamentally different from classical algorithms.
Post-Quantum Cryptography (PQC)
On the flip side, qubits also pose a threat to much of today’s cryptography. Powerful quantum algorithms – like Shor’s algorithm for integer factorization – can potentially break the public-key cryptosystems (RSA, ECC) that secure most internet communications. For example, a sufficiently advanced quantum computer could factor a 2048-bit RSA key (a basis of many secure protocols) in a matter of minutes, a task that would take a classical computer millions of years. This capability would render current encryption defunct. To address this looming threat, the security community is developing post-quantum cryptography (PQC) – new encryption algorithms that are believed to be resistant to attacks by quantum computers. Unlike quantum cryptography, PQC algorithms do not run on qubits; they are conventional algorithms (running on classical computers) but based on mathematical problems that even quantum computers should have a hard time solving (for example, lattice-based or hash-based cryptography, rather than factoring or discrete log). The goal is to roll out these quantum-resistant algorithms before large-scale quantum computers become available to adversaries. Many governments and standards bodies (like NIST) are already evaluating and standardizing PQC algorithms to replace or augment our current encryption toolkit. Essentially, post-quantum methods ensure that even if attackers develop quantum computers, the encrypted data remains secure. For cybersecurity professionals, staying informed about PQC is critical — it’s the proactive defense against future quantum attacks, complementing the more physics-based protections like QKD.
Conclusion
Quantum bits introduce new paradigms for securing (and attacking) information. Qubits and their properties – superposition enabling massive parallelism, entanglement enabling new protocols, and the measurement-disturbance principle enabling eavesdrop detection – are at the heart of both quantum computing’s power and its security implications. By understanding qubits at a high level, cybersecurity professionals can better prepare for the advent of quantum technologies. Whether deploying quantum key distribution for ultra-secure links or transitioning to post-quantum encryption algorithms, the knowledge of qubits and quantum principles will be increasingly crucial for protecting information in the quantum age.



